solve the following system of inequation by graphical method : 5x+4y≤40,x≥2,y≥3
Video Solution
Text Solution
The correct Answer is:N/a
For the inequation 5x+4y≤40.
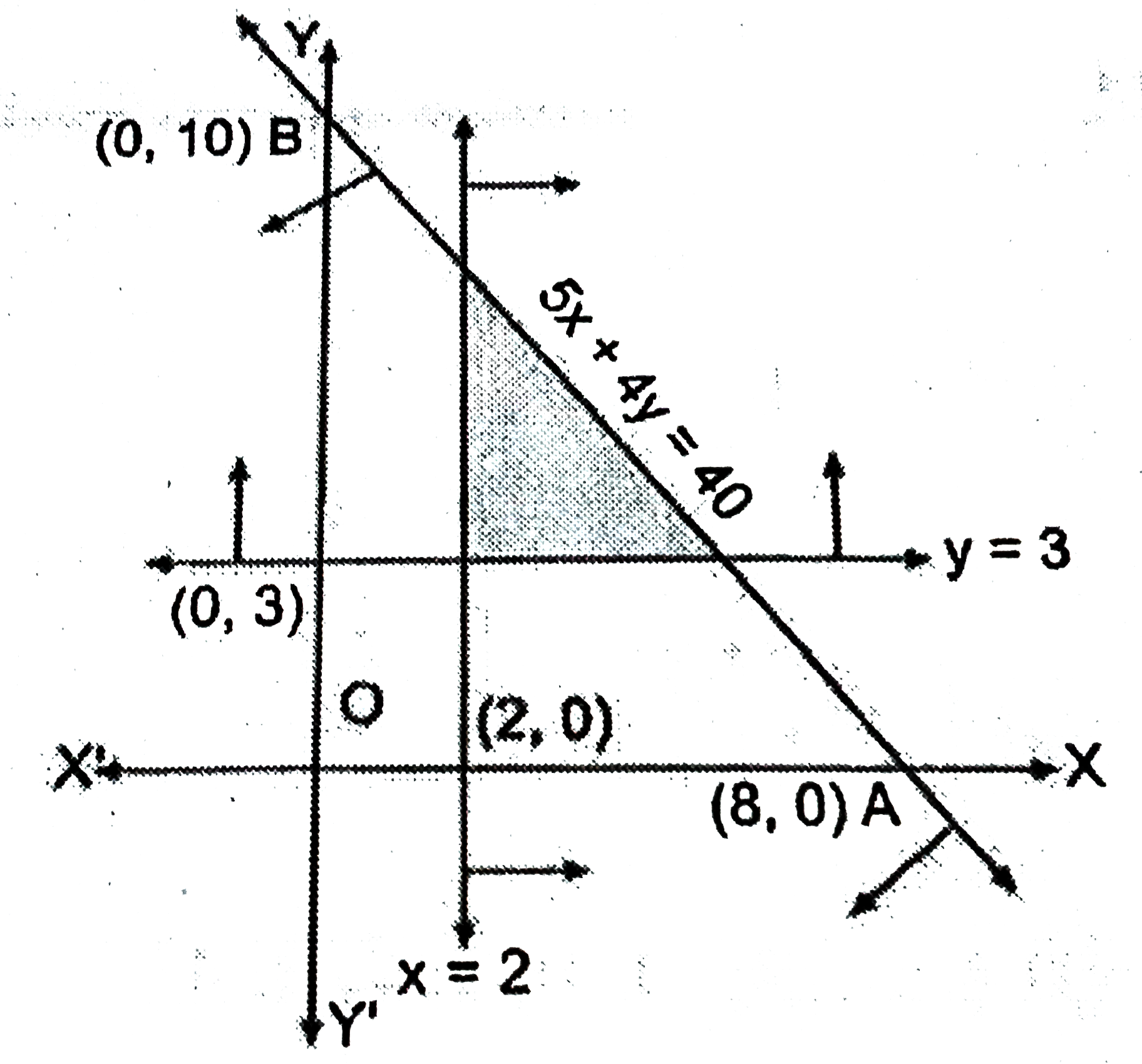
Corresponding equation 5x+4y=40 meets the X-axis and Y-axis at A (8, 0) and (0, 10) reapectively. Draw a thick line passing through A and B. Now put (0, 0) in the inequation, we get
0≤40
which is ture, i.e., inequation satisfies with (0, 0). Now AB divides the XY-plane into two parts, we shade that region in which (0, 0) lies.
For inequation x≥2:
Corresponding equation is x = 2 which is a line parallel to Y-axis and passes through (2, 0) .
The inequation does not satisfy with the point (0, 0). The line x = 2 divide the XY-plane into two parts. We shade that region in which (0, 0) does not lie.
For inequation y≥3:
Corresponding equation is y = 3, which is a line parallel to X-axis and passes throuth (0 ,3).
The inequation does not satisfy with the point (0, 0) . The line y = 3 divide the XY-plane into two parts.
Now the common shaded region of the given three inequation is the required solution.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR INEQUALITIESEXERCISE - EXERCISE76videos
LINEAR INEQUALITIES
- BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR INEQUALITIESEXERCISE - NCERT QUESTION51videos
LINEAR INEQUALITIES
- BOOK - NAGEEN PRAKASHANCHAPTER - LIMITS AND DERIVATIVESEXERCISE - Miscellaneous Exercise30videos
LIMITS AND DERIVATIVES
- BOOK - NAGEEN PRAKASHANCHAPTER - MATHEMATICAL REASONING EXERCISE - Misellaneous exercise7videos
MATHEMATICAL REASONING
Similar Questions
solve the following system of inequation by graphical method:
2x+3y≤6,3x+2y≤6,x≥0,y≥0View Solution5x+4y≤20,x≥1,y≥2
View SolutionSolve the following system of inequations graphically
x+y≤10,x+3y≤15,x≥0,y≥0View SolutionSolve the following system of inequalities graphically:
x+y≤200,x≤20,y≥4x,x≥0,y≥0.View SolutionSolve the following system of inequtions graphically.
x+3y≤12,33x+y≤12,x≥0,y≥0View Solutionx−y≤2,x+y≤4,x≥0,y≥
View SolutionFind the solution set of the following system of linear inequations.
5x+12y≥20
3x+8y≤40
x≥0
y≥0View SolutionSolve the system of inequalities graphically :x+y≤6,x+y≥4
View SolutionSolve the following system of inequations:
4x−5<11,−3x−4≥8.View Solutionsolve the inequation 2x−y≥3 by graphical method.
View Solution
