Question

Solve the inequalities graphically in two-dimensional plane: $3y-5x<30$

Explanation

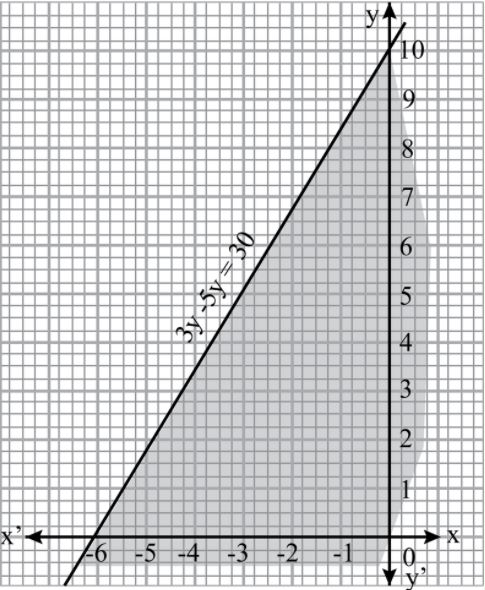
Given inequality is `3y-5x lt 30`.

Line that is dividing the region will be `3y-5x =30`

When `y=0, x = -6`

So, x-intercept is `(-6,0)`.

When `x=0, y = 10`

So, y-intercept is `(0,10)`.

Using these two intercepts, we can draw the line graphically.

Please refer to video for the graph.

If, we take point `(0,0)` in the shaded region, our inequality becomes,


Please refer to video for the graph.

`3(0)-5(0) lt 30=> 0 lt 30,`which is true.

So, the shaded region in the graph is the required region.