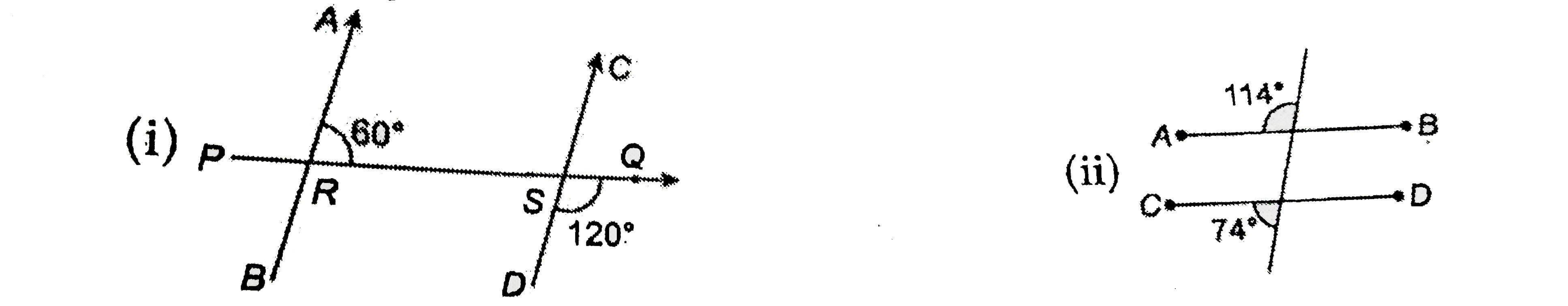State giving reason whether AB, CD and EF are parallel
The correct Answer is:Yes
Step by step video, text & image solution for State giving reason whether AB, CD and EF are parallel by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6 C20videos
LINES AND ANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - LINES AND ANGLESEXERCISE - Revision Exercise (very Short Answer Questions )10videos
LINES AND ANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6 A19videos
LINES AND ANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Revision Exercise12videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - NAGEEN PRAKASHANCHAPTER - NUMBER SYSTEMEXERCISE - Revision Exercise (short Answer Questions)10videos
NUMBER SYSTEM
Similar Questions
Knowledge Check
- Question 1 - Select One
AB, EF and CD are parallel lines. Given that EG = 5 cm, GC = 10 cm, AB = 15 cm and DC = 18 cm, find AC?A21 cmB25 cC18 cmD28 cm - Question 2 - Select One
In the given figure AB, CD and EF are three towers. The angle of elevation of the top of the tower CD from the top of the tower AB is 60∘ and that from EF is 30∘.BD=2√3m,CD:EF=5:4andDF=4m.
 A6 mB12 mC7 mDnone of the above
A6 mB12 mC7 mDnone of the above - Question 3 - Select One
ABCD is a trapezium such that AB and CD are parallel and BC⊥CD if ∠ADB=θ,Bc=pandCD=q, then AB is equal to
A(p2+q2sinθpcosθ+qsinθB(p2+q2)cosθpcosθ+qsinthetCp2+q2p2cosθ+q2sinθD(p2+q2)sinθ(pcosθ+qsinθ)
In a circle with centre O. AB and CD are parallel chords lying on opposite sides of a diameter parallel to them. If AB = 30 cm, CD - 48 cm and the distance between AB and CD is 27 cm, find the radius of the circle.
View Solution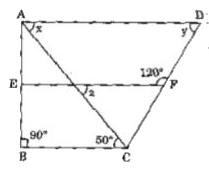
In the figure given above, AB CD trapezium. EF is parallel to AD and Angle y is equal to:View SolutionCan you find whether the lines EF , GH , KP , AB and CD are parallel or not by using other conditions of parallel lines ?
 View Solution
View SolutionABCD is a trapezium such that ABandCD are parallel and BC⊥CD. If /_ADB= theta , BC =p and CD=q, then AB is equal to
View SolutionABCD is a trapezium such that AB and CD are parallel and BC⊥CD. If ∠ADB=θ,BC=pandCD=q, then AB is equal to
View Solution