ABCD is a trapezium such that $A B and C D$ are parallel and $B C ⊥ C D$ . If /_ADB= theta , BC =p and CD=q, then AB is equal to

$((p^{2} + q^{2})) \frac{sin θ}{p cos θ + q sin θ}$

$\frac{p^{2} + q^{2} cos θ}{p cos θ + q sin θ}$

$\frac{p^{2} + q^{2}}{p^{2} cos θ + q^{2} sin θ}$

q $\frac{(p^{2} + q^{2})}{{(p^{2} cos θ + q^{2} sin θ)}^{2}}$

Video Solution

Text Solution

Verified by Experts

Applying sine rule in $Δ A B D$ ,

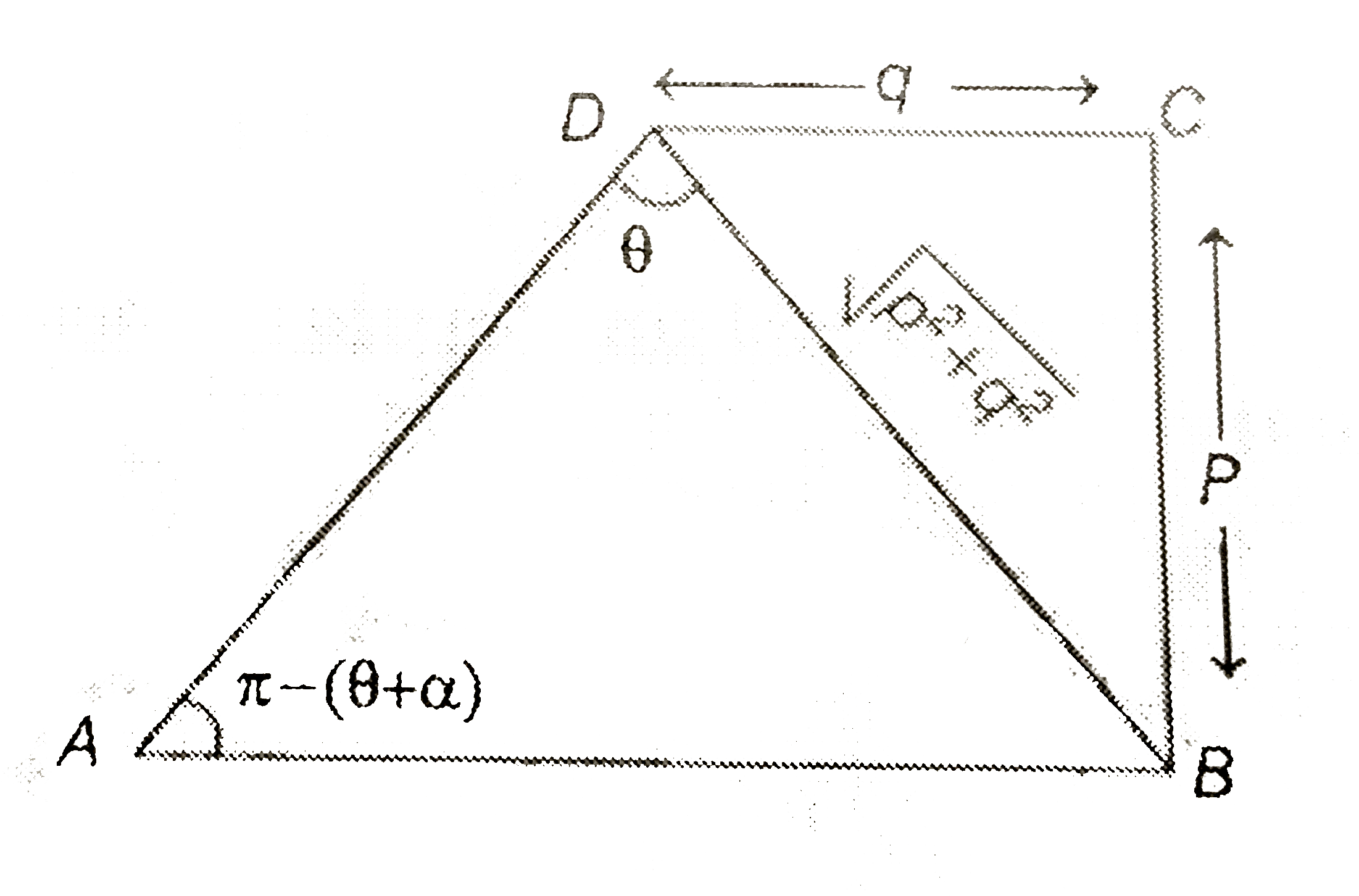
$\frac{A B}{sin θ} = \frac{\sqrt{p^{2} + q^{2}}}{sin {π - (θ + α)}}$
$\Rightarrow \frac{A B}{sin θ} = \frac{\sqrt{p^{2} + q^{2}}}{sin (θ + α)}$
$\Rightarrow A B = \frac{\sqrt{p^{2} + q^{2}} sin θ}{sin θ cos α + cos θ sin α} [∴ cos α = \frac{q}{\sqrt{p^{2} + q^{2}}}]$
$= \frac{(p^{2} + a^{2} sin θ)}{p cos 0 + q sin θ}$
Alternate Solotion
Let AB=x

In $Δ D A M, tan (π θ - α) = \frac{p}{x - q}$
$\Rightarrow tan (θ + α) = \frac{p}{q - x}$
$\Rightarrow q - x p cot (θ + α)$
$\Rightarrow x = q - p cos (θ + α)$
$= p - q (\frac{cot θ cot α - 1}{cot α + cot θ}) = [∴ cot α = \frac{q}{p}]$
$= q - p ⎛ ⎝ \frac{\frac{q}{p} cot θ - 1}{\frac{q}{p} + cot θ} ⎞ ⎠ = q - p (\frac{q cot θ - p}{q + p cot θ})$
$= q - p (\frac{q cos θ - p sin θ}{q sin θ + p cos θ})$
$\Rightarrow x = \frac{q^{2} sin θ + q p cos θ - p q cos θ + p^{2} sin θ}{p cos θ + q sin θ}$
$\Rightarrow A B = \frac{(p^{2} + q^{2})}{p cos θ + q sin θ}$

Updated on:21/07/2023