State giving reasons, whether the following pairs of triangles are congruent or not: ΔDEF in which ∠E=48∘,DE=6cm,EF=8cm and ΔMNR in which ∠R=48∘,MN=6cm,MR=8cm
The correct Answer is:No
To determine whether the triangles ΔDEF and ΔMNR are congruent, we will analyze the given information step by step.
Step 1: Identify the given information for both triangles.
- For ΔDEF:
- ∠E=48∘
- DE=6cm
- EF=8cm
- For ΔMNR:
- ∠R=48∘
- MN=6cm
- MR=8cm
Step 2: Compare the angles and sides of both triangles.
- Both triangles have one angle equal to 48∘:
- ∠E in ΔDEF and ∠R in ΔMNR.
- Both triangles have two sides of equal length:
- DE=6cm and MN=6cm
- EF=8cm and MR=8cm
Step 3: Check the congruency criteria.
To establish congruency, we can use the Angle-Side-Side (ASS) criterion, but this criterion does not guarantee congruency because the angle is not between the two sides.
- In ΔDEF, the angle E is not between the sides DE and EF.
- In ΔMNR, the angle R is not between the sides MN and MR.
Step 4: Conclusion.
Since the angle E in ΔDEF is not between the sides DE and EF, and similarly for ΔMNR, we cannot conclude that the triangles are congruent based on the information provided.
Thus, ΔDEF is not congruent to ΔMNR.
Final Answer:
The triangles ΔDEF and ΔMNR are not congruent.
---
- For ΔDEF:
- ∠E=48∘
- DE=6cm
- EF=8cm
- ∠R=48∘
- MN=6cm
- MR=8cm
- Both triangles have one angle equal to 48∘:
- ∠E in ΔDEF and ∠R in ΔMNR.
- DE=6cm and MN=6cm
- EF=8cm and MR=8cm
To establish congruency, we can use the Angle-Side-Side (ASS) criterion, but this criterion does not guarantee congruency because the angle is not between the two sides.
- In ΔMNR, the angle R is not between the sides MN and MR.
Since the angle E in ΔDEF is not between the sides DE and EF, and similarly for ΔMNR, we cannot conclude that the triangles are congruent based on the information provided.
The triangles ΔDEF and ΔMNR are not congruent.
Topper's Solved these Questions
Similar Questions
State giving reasons, whether the following pairs of triangles are congruent or not: ΔABC in which AB=3 cm ∠A=90∘, BC=5 cm and ΔKLM in which KM=3 cm ∠K=90∘ cm, 1,M=5cm
View SolutionState giving reasons, whether the following pairs of triangles are congruent or not: ΔABC in which ∠A=50∘,∠B=60∘,BC=4.5 cm and ΔDEFo in which ∠E=60∘,EF=4.5cm,∠F=70∘
View SolutionState giving reasons, whether the following pairs of triangles are congruent or not: ΔKLM in which KM=4 cm ∠K=75∘,∠M=40∘ and ΔPQR in which PR=4 cm, ∠Q=65∘,∠R=40∘.
View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.
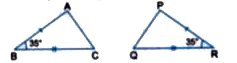
View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.
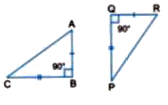
View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.

View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.
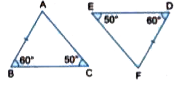
View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.

View SolutionConvert the following values as indicated.
6 m 8 cm into cm
View SolutionConstructαΔABC in which AB=4.8cm,BC=5cmandCA=5.4cm.
View Solution
