State giving reasons, whether the following pairs of triangles are congruent or not: ΔKLM in which KM=4 cm ∠K=75∘,∠M=40∘ and ΔPQR in which PR=4 cm, ∠Q=65∘,∠R=40∘.
The correct Answer is:Yes,(ASA)
To determine whether the triangles ΔKLM and ΔPQR are congruent, we will use the information provided and apply the criteria for triangle congruence.
1. Identify Given Information:
- For triangle KLM:
- KM=4cm
- ∠K=75∘
- ∠M=40∘
- For triangle PQR:
- PR=4cm
- ∠Q=65∘
- ∠R=40∘
2. Calculate the Missing Angle in Triangle PQR:
- The sum of angles in a triangle is 180∘.
- For triangle PQR:
∠P+∠Q+∠R=180∘
∠P+65∘+40∘=180∘
∠P+105∘=180∘
∠P=180∘−105∘=75∘
3. Compare Corresponding Angles:
- Now we have:
- ∠K=75∘ (from KLM)
- ∠P=75∘ (calculated for PQR)
- ∠M=40∘ (from KLM)
- ∠R=40∘ (from PQR)
4. Compare Corresponding Sides:
- We also have:
- KM=4cm (from KLM)
- PR=4cm (from PQR)
5. Establish Congruence:
- We can now establish that:
- ∠K=∠P
- ∠M=∠R
- KM=PR
- By the Angle-Side-Angle (ASA) congruence criterion, since two angles and the included side of one triangle are equal to two angles and the included side of another triangle, we conclude that:
ΔKLM≅ΔPQR
Conclusion:
The triangles ΔKLM and ΔPQR are congruent.
---
- For triangle KLM:
- KM=4cm
- ∠K=75∘
- ∠M=40∘
- For triangle PQR:
- PR=4cm
- ∠Q=65∘
- ∠R=40∘
- The sum of angles in a triangle is 180∘.
- For triangle PQR:
∠P+∠Q+∠R=180∘
∠P+65∘+40∘=180∘
∠P+105∘=180∘
∠P=180∘−105∘=75∘
- Now we have:
- ∠K=75∘ (from KLM)
- ∠P=75∘ (calculated for PQR)
- ∠M=40∘ (from KLM)
- ∠R=40∘ (from PQR)
- We also have:
- KM=4cm (from KLM)
- PR=4cm (from PQR)
- We can now establish that:
- ∠K=∠P
- ∠M=∠R
- KM=PR
- By the Angle-Side-Angle (ASA) congruence criterion, since two angles and the included side of one triangle are equal to two angles and the included side of another triangle, we conclude that:
ΔKLM≅ΔPQR
The triangles ΔKLM and ΔPQR are congruent.
Topper's Solved these Questions
Similar Questions
State giving reasons, whether the following pairs of triangles are congruent or not: ΔABC in which ∠A=50∘,∠B=60∘,BC=4.5 cm and ΔDEFo in which ∠E=60∘,EF=4.5cm,∠F=70∘
View SolutionState giving reasons, whether the following pairs of triangles are congruent or not: ΔABC in which AB=3 cm ∠A=90∘, BC=5 cm and ΔKLM in which KM=3 cm ∠K=90∘ cm, 1,M=5cm
View SolutionState giving reasons, whether the following pairs of triangles are congruent or not: ΔDEF in which ∠E=48∘,DE=6cm,EF=8cm and ΔMNR in which ∠R=48∘,MN=6cm,MR=8cm
View SolutionConstruct a triangle PQR with PQ = 4 cm, ∠P=75∘,and∠R=65∘.
View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.

View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.
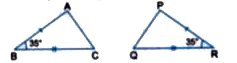
View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.
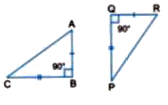
View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.

View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.
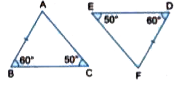
View SolutionConstruet aΔABC in which AB=4cm,BC=4.6cmand∠B=75∘.
View Solution
