State the basic proportionality theorem.
Step-by-Step Text Solution:
1. Understanding the Basic Proportionality Theorem (BPT): The Basic Proportionality Theorem, also known as Thales' theorem, is a fundamental concept in geometry, particularly in the study of triangles.
2. Statement of the Theorem: The theorem states that if a line is drawn parallel to one side of a triangle, it will intersect the other two sides of the triangle at distinct points.
3. Division in Proportion: This line divides the two sides of the triangle in proportion. Specifically, if the triangle is ABC, and a line DE is drawn parallel to side BC, intersecting sides AB and AC at points D and E respectively, then the following relationship holds:
ADDB=AEEC
This means that the ratio of the lengths of the segments on one side of the triangle is equal to the ratio of the lengths of the segments on the other side.
4. Conclusion: Thus, the Basic Proportionality Theorem establishes a relationship between the segments created by a line parallel to one side of a triangle, confirming that they are proportional.
---
ADDB=AEEC
This means that the ratio of the lengths of the segments on one side of the triangle is equal to the ratio of the lengths of the segments on the other side.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Multiple Choice Questions (Mcq)53videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTPILE-CHOICE QUESTIONS (MCQ) ( MATCHING OF COLUMNS)1videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7D22videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 1127videos
T-RATIOS OF SOME PARTICULAR ANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself20videos
TRIGONOMETRIC IDENTITIES
Similar Questions
Knowledge Check
- Question 1 - Select One
Thales theorem is given by a greek mathematician. According to this theorem, if a line is drawn parallel to one side of a triangle then it divides the other two sides in the same ratio. This theorem is also known as Basic Proportionality Theorem.
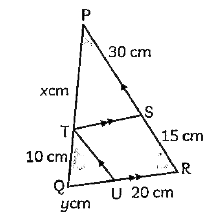
Here, the value of x is :A20 cmB15 cmC5 cmD10 cm
Thales Theorem ( Basic Proportionality Theorem)
View SolutionConverse of Basis proportionality theorem : If a line divides any two sides of a triangle in the same ratio; then the line must be parallel to the third side.
View SolutionBasic Proportionality Theorem (Thale's Theorem)|Converse Of Basic Proportionality Theorem|Example|Questions|OMR
View SolutionBasic Proportionality Theorem|Converse Of BPT (Basic Proportionality Theorem) (Thales Theorem)|NCERT Example Questions
View SolutionTriangles|Basic Proportionality Theorem(BPL)Thales Theorem|Converse Of (Basic Proportionality Theorem(BPL))Thales Theorem|Criteria For Similarity Of Triangles |Pythagoras Theorem And Its Converse
View SolutionOMR|Converse Of Basic Proportionality Theorem|Questions|Criteria For Similarity Of Triangles|Theorem|Questions|Theorem
View SolutionState and prove Basic Proportionality Theoram (Thales Theoram)
View Solution

