Students of a school are standing in rows and columns in their playground for a drill practice . A, B, C and D are the positions of four students as shown in figure . Is it possible to place Jaspal inn the drill in such a way that he is equidistant from each of the four students A, B C and D ? If so, what should be his position ?
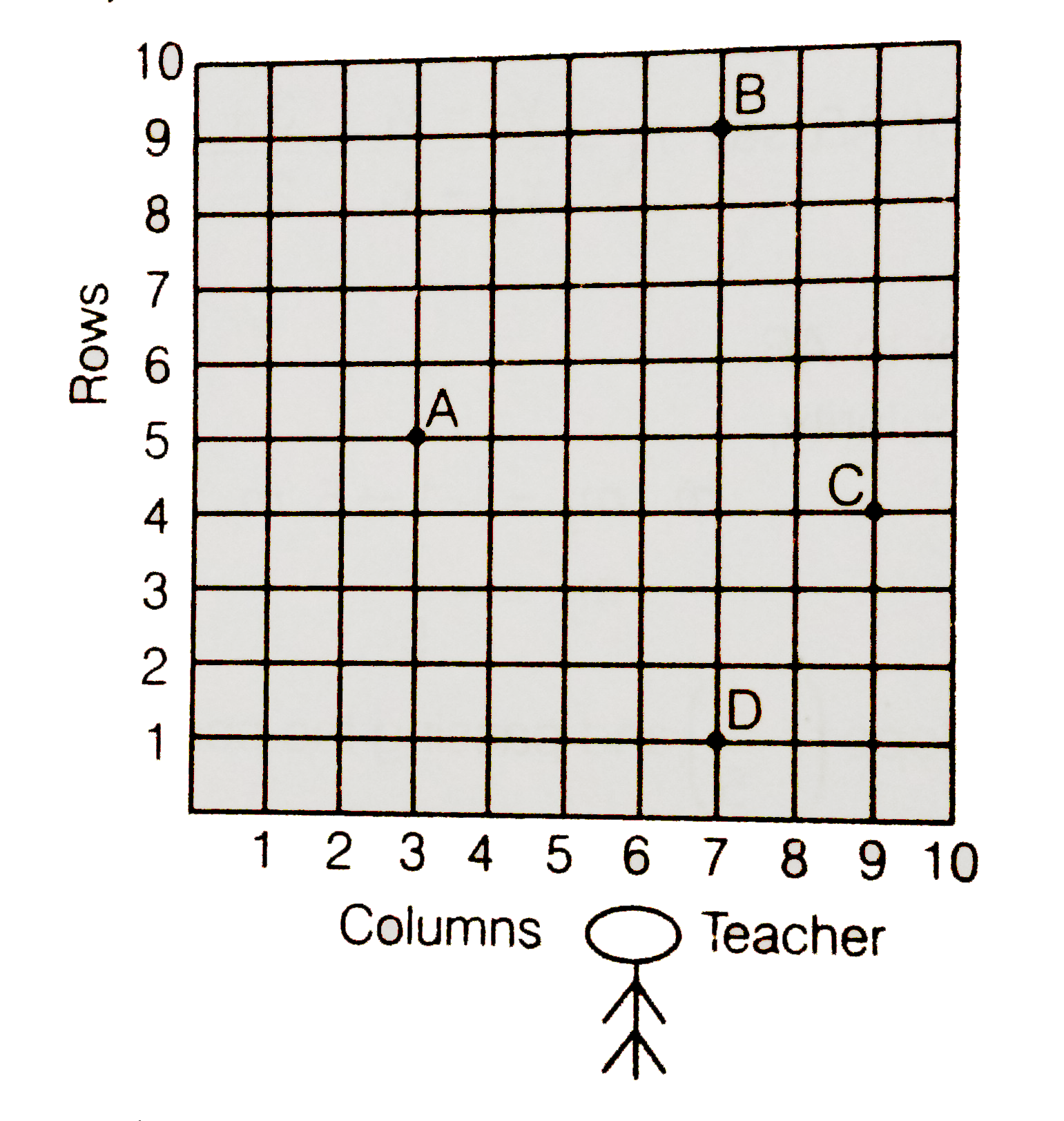
Yes , from the figure we observe that the positions of four students A, B , C and D are (3,5),(7,9) , (11,5) and (7,1) respectively i.e., these are four vertices of a a quadrillateral . Now, we find the type of the this quadrilateral . For this , we will all its sides.

Now, AB =√(7−3)2+(9−5)2
[ by distance formula , d =√(x2−x1)2+(y2−y1)2]
AB =√(4)2+(4)2=√16+16
AB=4√2
BC =√(11−7)2+(5−9)2=√(4)2+(−4)2
=√16+16=4√2
and DA =√(3−7)2+(5−1)2=√(−4)2+(4)2
=√16+16=4√2
we see that , AB=BC=CD=DA i.e., all siedes are equal.
Now , we find lenght of both diagonals .
AC=√(11−3)2+(5−5)2=√(8)2+0=8
and BD =√(7−7)2+(1−9)2=√0+(−8)2=8
Here , AC=BD
Since, AB=BC=CD=DAandAC=BD
Which represent a square . Also known the diagonals of a square bisect each other . SO , P be position of jaspal in which he is equidistant from each of the four students A,B, C and D.
∴ Coordinates of points P = Mid - point of AC
(3+112,5+52)≡(142,102)≡(7,5)
[since , mid - point of a line segment having points (x1,y1)and(x2,y2)=(x1+y12,x2+y22)]
Hince , the required position of Jaspal is (7,5).
Topper's Solved these Questions
- COORDINATE GEOMETRYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 7.3 Very Short Answer Type Questions
20 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions
7 Videos
- INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONSEXERCISE - LONG ANSWER TYPES QUESTIONS
18 Videos
Similar Questions
Find the unknown entries a,b,c,d,e and f in the following distribution of heights of students in a class
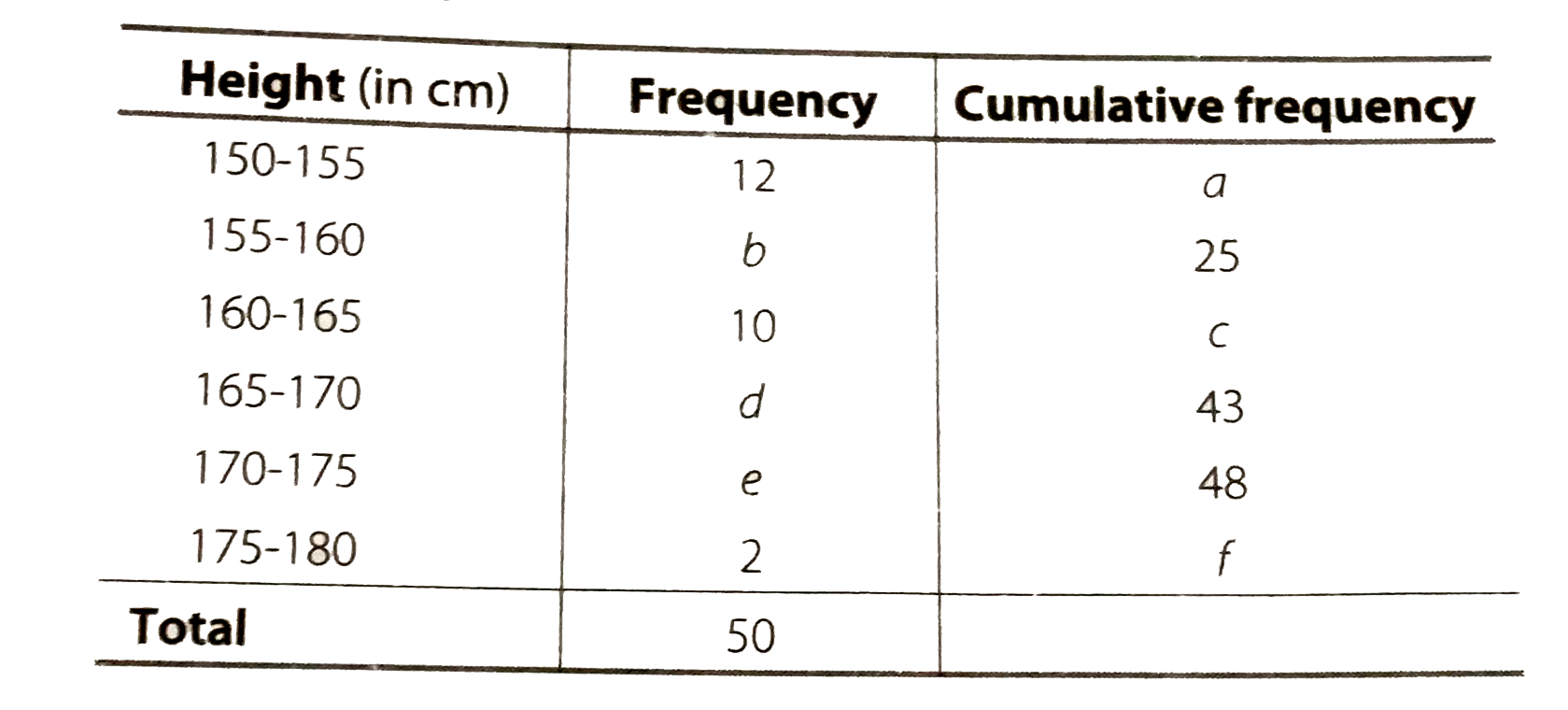
View SolutionFind the unknown entries a,b,c,d,e and f in the following distribution of heights of students in a class

View SolutionThe number of planes that are equidistant from four non-coplanar points is a. 3 b. 4 c. 7 d. 9
View SolutionThe sides BA and DC of a quadrilateral ABCD are produced as shown in Figure. Prove that a+b=x+y. Figure
View SolutionThe students of a class are made to stand in rows. If 3 students are extra in a row; there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.
View SolutionThe students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row there would be 2 rows more. Find the number of students in the class.
View SolutionThe students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row there would be 2 rows more. Find the number of students in the class.
View SolutionStudents of a class are made to stand in rows. If one student is extra in a raw, there would be 2 rows less. If one student is less in a row there would be 3 rows more. Find the number of students in the class.
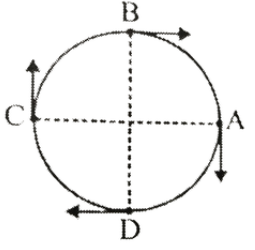
View SolutionFour particles A, B, C and D are moving with constant speed v each. At the instant shown relative velocity of A with respect to B, C and D are in directions :-
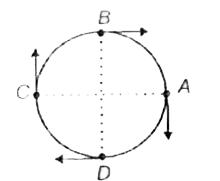
View SolutionFour particles A, B, C and D are moving with constant speed v each at the instant shown relative velocity of A with respect to B, C and D are in directions
View Solution
