Suppose be three mutually exclusive events such that .
P(none of ) equals
0
1-
None of these
The correct Answer is:(b)
To find the probability that none of the events E1,E2, and E3 occur, we can follow these steps:
Step 1: Understand the Events
Given that E1,E2, and E3 are mutually exclusive events, it means that the occurrence of one event excludes the occurrence of the others.
Step 2: Write the Probability of None of the Events
The probability of none of the events occurring can be expressed as:
P(none of E1,E2,E3)=P(Ec1∩Ec2∩Ec3)
Where Eci denotes the complement of event Ei.
Step 3: Use the Complement Rule
Using the complement rule, we can express the probability of none of the events occurring in terms of the probability of at least one event occurring:
P(Ec1∩Ec2∩Ec3)=1−P(E1∪E2∪E3)
Step 4: Calculate P(E1∪E2∪E3)
Since the events are mutually exclusive, the probability of their union can be calculated as:
P(E1∪E2∪E3)=P(E1)+P(E2)+P(E3)=p1+p2+p3
Step 5: Substitute Back
Now, substituting this back into our equation for the probability of none of the events:
P(none of E1,E2,E3)=1−(p1+p2+p3)
Final Answer
Thus, the probability that none of the events E1,E2, and E3 occurs is:
P(none of E1,E2,E3)=1−(p1+p2+p3)
---
Given that E1,E2, and E3 are mutually exclusive events, it means that the occurrence of one event excludes the occurrence of the others.
The probability of none of the events occurring can be expressed as:
P(none of E1,E2,E3)=P(Ec1∩Ec2∩Ec3)
Where Eci denotes the complement of event Ei.
Using the complement rule, we can express the probability of none of the events occurring in terms of the probability of at least one event occurring:
P(Ec1∩Ec2∩Ec3)=1−P(E1∪E2∪E3)
Since the events are mutually exclusive, the probability of their union can be calculated as:
P(E1∪E2∪E3)=P(E1)+P(E2)+P(E3)=p1+p2+p3
Now, substituting this back into our equation for the probability of none of the events:
P(none of E1,E2,E3)=1−(p1+p2+p3)
Thus, the probability that none of the events E1,E2, and E3 occurs is:
P(none of E1,E2,E3)=1−(p1+p2+p3)
Topper's Solved these Questions
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Single Integer Answer Type Questions)
10 Videos
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Probability Exercise 5: Match Type Questions
5 Videos
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
28 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
Similar Questions
Suppose E1,E2andE3 be three mutually exclusive events such that P(Ei)=pi for i=1,2,3.
If p1,p2andp3 are the roots of 27x3−27x2+ax−1=0 the value of a is
View SolutionSuppose E1,E2andE3 be three mutually exclusive events such that P(Ei)=pi for i=1,2,3.
P(E1∩¯¯¯¯E2)+P(E2∩¯¯¯¯E3)+P(E3∩¯¯¯¯E1) equals
View Solution
Knowledge Check
Let E1andE2 are two mutually exclusive and exhaustive events. If odds are 2:3 against E1 then odds in favour of E2 are
A3:2B1:3C3:1D2:3If A,B,C are three mutually exclusive and exhaustive events of an experiment such 3P(A) = 2I = P(C ) , the P(A) is equal to .
A111B211C511D611
Statement -1 : Let E1,E2,E3 be three events such that P(E1)+P(E2)+P(E3)=1, then E1,E2,E3 are exhaustive events.
Statement-2 if the events E1,E2 and E3 be exhaustive events, then P(E1∪E2∪E3)=1
View SolutionLet H1,H2,...,Hn be mutually exclusive events with P(Hi)>0,i=1,2,..........n. Let E be any other event with 0<P(E) Statement I P(Hi∣E)>P(E∣Hi.P(Hi) for i=1,2,.......,n statement II n∑i=1P(Hi)=1
View SolutionSuppose that E1 and E2 are two events of a random experiment such that P(E1)=14,P(E2∣E1)=12andP(E1∣E2)=14. Observe the lists given below :
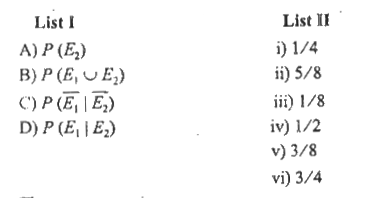
The correct matching of the list I from the list II is :
View SolutionLet p (x) be a polynomial with real coefficient and p(x)=x2+2x+1. Find P (1).
View SolutionIf EandF are two events such that P(E∪F)=0.6,P(E∩F)=0.3,P(F)=0.2. Find P(notE) .
View SolutionIf E1 and E2 are two events such that P(E1)=1/4, P(E2/E1)=1/2 and P(E1/E2)=1/4, then
View Solution
