If E1 and E2 are two events such that P(E1)=1/4, P(E2/E1)=1/2 and P(E1/E2)=1/4, then
then E1 and E2 are independent
E1 and E2 are exhaustive
E2 is twice as likely to occur as E1
Probabilites of the events E1∩E2, E1 and E2 are in G.P.
The correct Answer is:A, C, D
(a,c,d) P(E2/E1)=P(E1∩E2)P(E1)
12=P(E1∩E2)1/4
⇒P(E1∩E2)=18=P(E2)⋅P(E1/E2)
=P(E2)⋅14
⇒P(E2)=12
Since P(E1∩E2)=18=P(E1)⋅P(E1)⋅P(E2), events are independent
Also P(E1∪E2)=12+14−18=58
⇒E1 and E2 are not exhaustive.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - PROBABILITYEXERCISE - Comprehension2videos
PROBABILITY
- BOOK - CENGAGE ENGLISHCHAPTER - PROBABILITYEXERCISE - Comprehension2videos
PROBABILITY
- BOOK - CENGAGE ENGLISHCHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - Sovled Examples22videos
PRINCIPLE OF MATHEMATICAL INDUCTION
- BOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY I EXERCISE - JEE Advanced7videos
PROBABILITY I
Similar Questions
If E1 and E2 be two events such that P(E1)=0.3,P(E2)=0.2 and P(E1∩E2)=0.1, then find:
(i) P(¯¯¯E1∩E2) (ii) P(E1∩¯¯¯E2)View SolutionSuppose that E1 and E2 are two events of a random experiment such that P(E1)=14,P(E2∣E1)=12andP(E1∣E2)=14. Observe the lists given below :
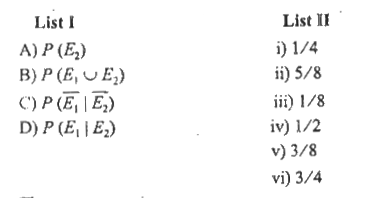
The correct matching of the list I from the list II is :View Solution
Knowledge Check
- Question 1 - Select One
Let E and F be the events such that, P(E)=13,P(F)=14andP(E∩F)=15, find P(¯¯¯F¯¯¯E).
A3740B34C47DNone of these
Let E1andE2 be two independent events such that P(E1)=P1 and P(E2)=P2, describe in words of the events whose probabilities are
(i) P1P2 (ii) (1−P1)P2
(iii) 1−(1−P1)(1−P2) (iv) P1+P2−2P1P2View SolutionIf E and F are two events such that P(E)=14,P(F)=12andP(E∩F)=18,then find P(E'∩F')
View SolutionIf E and F are events such that P(E)=14,P(F)=12andP(EandF)=18, find P(EorF)
View SolutionFor two events E1 and E2,P(E1)=12,P(E2)=13 and P(E1∩E2)=110. Find:
(i) P(E1orE2)
(ii) P(E1but notE2)
(iii) P(E2but notE1)
View SolutionIf e1,e2,e3 and e4 are the four elementary outcomes in a sample space and P(e1)=0.1,P(e2)=0.5,and P(e3)=0.1, then the probability of e4 is ……
View SolutionIf E and F are events such that P(E)=14,P(F)=12andP(EandF)=18, find (i) P(EorF), (ii) P(−Eand−F).
View SolutionIf E and F are events such that P(E)=14,P(F)=12 and P(EandF)=18, find (i) P(EorF) (ii) P (not E and not F).
View Solution

