Suppose n is a natural number such that ∣∣i+2i2+3i3+......+nin∣∣=18√2 where i is the square root of −1. Then n is Solution in Tamil
9
18
36
72
The correct Answer is:C
(c) S=i+2i2+3i3+…….+nin………..(i)
∴iS=i2+2i3+3i4+…….+nin−1…………(ii)
Subtracting, we get S(1−i)=i+i2+i3+………..+in−nin+1
=i(1−in)1−i−nin+1
Now put the values of n and verify.
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer
11 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column
1 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
87 Videos
Similar Questions
Complex numbers whose real and imaginary parts x and y are integers and satisfy the equation 3x2−|xy|−2y2+7=0
View Solutionz1, z2, z3 are vertices of a triangle. Match the condition in List I with type of triangle in List II.
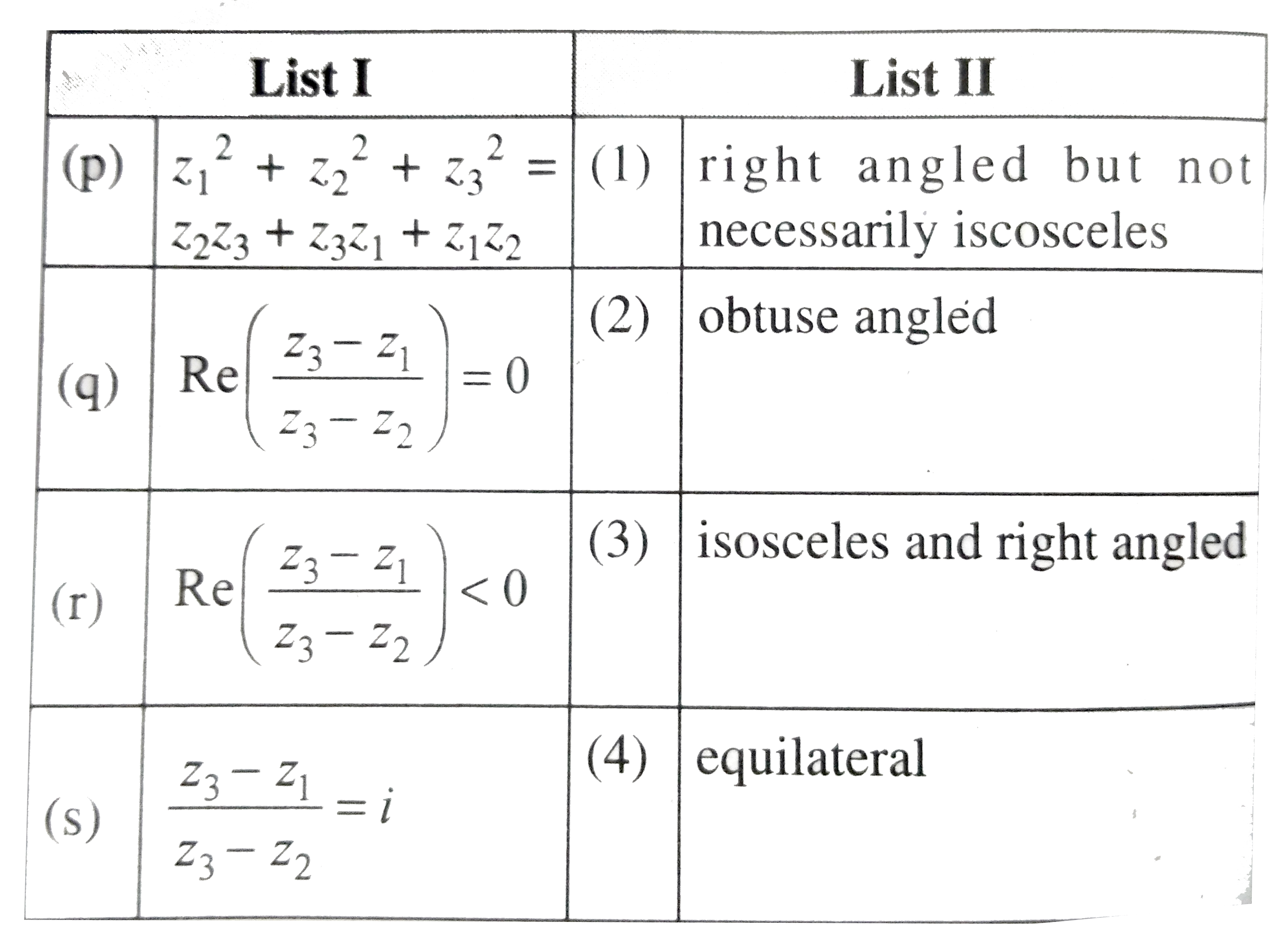
Codes
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
View Solution(1+i)(1+2i)(1+3i)............(1+ni)=alpha+i beta, then the value of 2.5.10......(1+n^(2))=alpha^(2)+beta^(2)
View SolutionSuppose n is a natural number such that |i+2i^(2)+3i^(3)+......+ni^(n)|=18sqrt(2) where i is the square root of -1. Then n is
View SolutionIf (1+i)(1+2i)(1+3i)...(1+ni)=a+ib then 2xx5xx10xx...(1+n^(2))=
View SolutionIf (1+i)(1+2i)(1+3i),…(1+ni)=a+ib then the value of 2×5×10×…×(1+n2) is-
View SolutionIf (1 + i)(1 + 2i)(1 + 3i)….(1 + ni) = x + iy, then 2.5.10…(1+n2)is
View SolutionIf (1−i)(1−2i)(1−3i)…..(1−ni)=x−iy , then 2.5.10……(1+n2)=
View SolutionIf (1−i)(1−2i)(1−3i)…..(1−ni)=x−iy , then 2.5.10……(1+n2)=
View SolutionIf (1+i)(1+2i)(1+3i).......(1+ni)=x+iy, then 2.5.10.........(1+n2)=
View SolutionIf (1+i)(1+2i)(1+3i)…….(1+ni)=a+ib, then 2×5×10×………×(1+n2) is equal to
View SolutionIf (1+i)(1+2i)(1+3i)…..(1+ni)=x+iy then 2.5.10 …. (1+n2)=
View Solution(1 + i) (1 + 2i) (1 + 3i) ... (1 + ni) = x + iy எனில், 2.5.10...(1+n2) -ன் மதிப்பு
View SolutionSuppose n is a natural number such that | i+2i^2+3i^3 +…+ ni^n|=18sqrt2 , Where i=sqrt(-1) is . Then the value of n is
View Solution
