Suppose OABC is a reatangle in the xy-plane where O is the origin and A, B lie on the parabola y=x2.Then C must lie on the curve
y=x2+2
y=2x2+1
y=−x2+2
y=−2x2+1
The correct Answer is:A
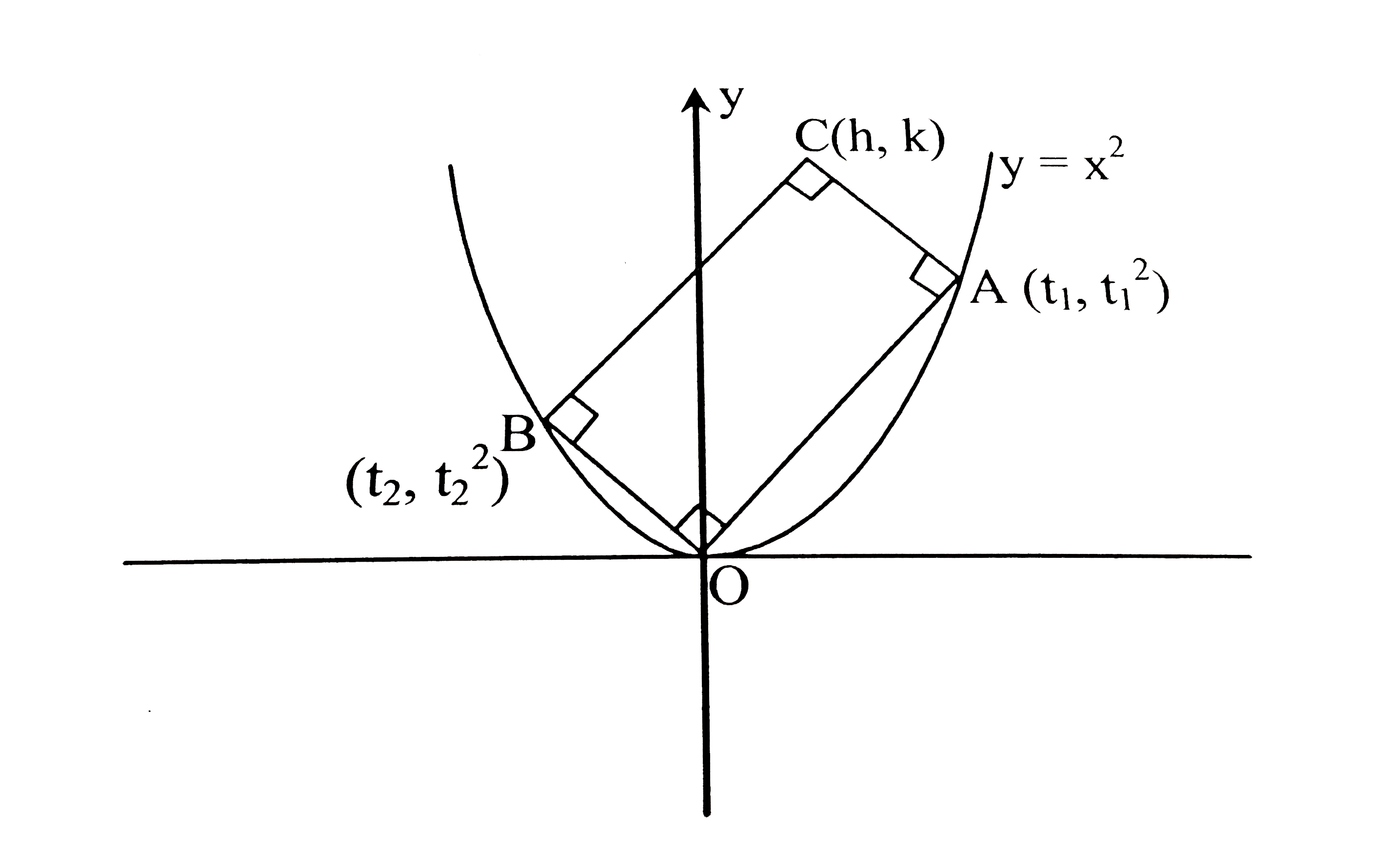
∵OB⊥OA
So,t1t2=−1
Nowh2=t1+t22
t2+t2=h . . . (1)
alsot21+t22=k
(t1+t2)2−2t1t2=k
h2+2=k
locus is x2+2=y
Similar Questions
The area (in sq. units) of the largest rectangle ABCD whose vertices A and B lie on the x - axis and vertices C and D lie on the parabola, y=x2−1 below the x - axis, is :
View SolutionEllipse x2a2+y2b2=1,(a>b), If the extremities of the latus rectum of the with positive ordinates lie on the parabola x2=3(y+3), then length of the transverse axis of ellipse is
View Solution
Knowledge Check
Which of the following points lie on the parabola x2=4ay
Ax=at2,y=2atBx=2at,y=atCx=2at2,y=atDx=2at,y=at2Tangents are drawn from the origin to the curve y=sin x then ,the point of contact lie on the curve is
Ay2=x21−x2By2=x21+yCx2=y21+y2Dy2=x21+x2The points of contact of the tangents drawn from the origin to the curve y = sin x lie on the curve
Ax2−y2=xyBx2+y2=x2y2Cx2−y2=x2y2DNone of these
find the area of the quadrilateral whose vertices lie at the points of intersection of the parabola y=4−x2 with the axis and the straight line y=3x.
View SolutionThe points of contact of the tangents drawn from the origin to the curve y=sinx, lie on the curve
View SolutionTangents are drawn from origin to the curve y=sin+cosx·Then their points of contact lie on the curve
View SolutionLet A(4,−4) and B(9,6) be points on the parabola y2=4x. Let C be chosen on the on the arc AOB of the parabola where O is the origin such that the area of ΔACB is maximum. Then the area (in sq. units) of ΔACB is :
View SolutionTangents are drawn from the origin to the curve y=cosX. Their points of contact lie on
View Solution
