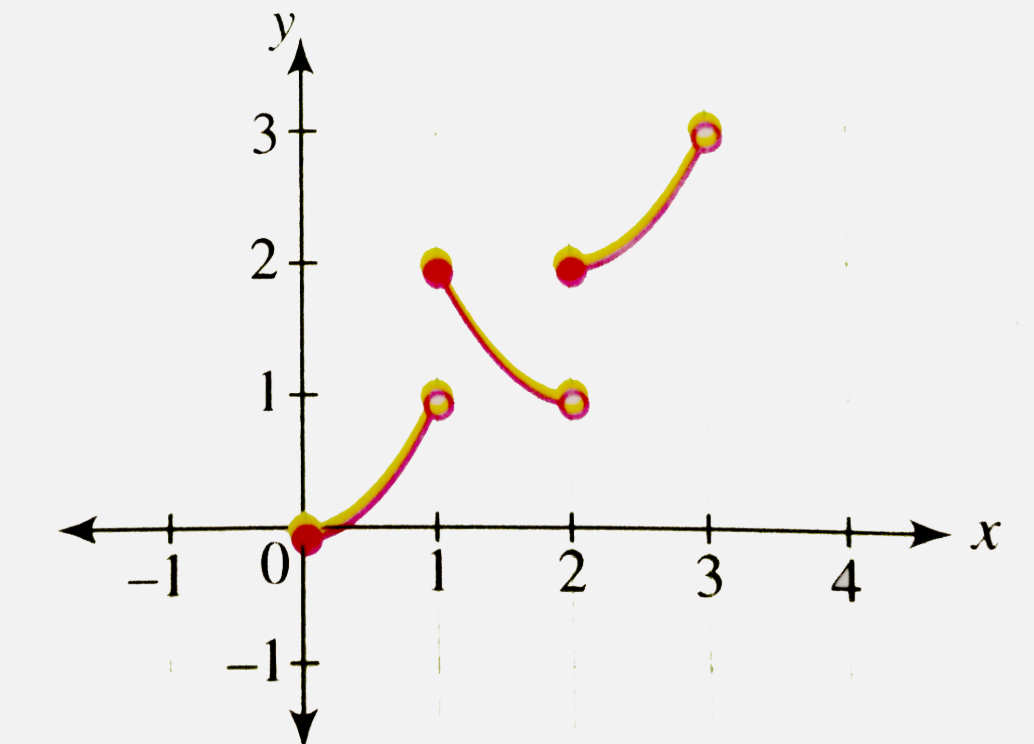
Suppose that f is even, periodic function with period 2, and that f(x) = x for all x in the interval [0, 1]. Then draw the graph of y = f(x). Solution in Tamil
Since f is periodic with period 2and f(x)=x→x∈[0,1], also f(x) is even
So the graph is symmetrical about the y-axis.
So the graph of f(x) is as shown.

Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBOOK - CENGAGECHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercise
18 Videos
- FUNCTIONSBOOK - CENGAGECHAPTER - FUNCTIONSEXERCISE - Question Bank
21 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
Similar Questions
Does the following graph pass the vertical or horizontal line test ?
View SolutionIf there are four distinct real numbers satisfying thẻ equation ∣∣x2−4x−7∣∣=n, then number of integers in the range of n is
View SolutionDraw the graph of y=tan−1x+cot−1x
View SolutionIf f(x+y)=f(x).f(y) for all real x,yandf(0)≠0, then prove that the function g(x)=f(x)1+{f(x)}2 is an even function.
View SolutionSuppose that f is an even, periodic function with period 2,andthatf(x)=x for all x in the interval [0,1] . The values of [10f(3.14)] is(where [.] represents the greatest integer function) ______
View SolutionSuppose that f is even, periodic function with period 2, and that f(x) = x for all x in the interval [0, 1]. Then draw the graph of y = f(x).
View SolutionGiven f(x) is a periodic function with period 2 and it is defined as
f(x)=⎧⎨⎩[cosπx2]+1,0<x<12−x,1≤x<2
Here [⋅] represents the greatest integer ≤x. If f(0)=1, then draw the graph of the function for x∈[−2,2].
View SolutionAn even periodic function f:R→R with period 4 is such that
f(x)={max.(|x|,x2),0≤x<1x,1≤x≤2. Then draw the graph of y=f(x) for x∈R
View SolutionIf f is a function of real variable x satisfying f(x+4)−f(x+2)+f(x)=0 , then f is periodic function with period:
View SolutionA function f is said to be periodic if it repeats its nature after certain interval and that interval is called period of the function. If T be the period of f(x), then f(x + T) = f(x). For example f(x) = tan x is periodic with period π. Then find the period of f(x) that satisfies the following condition.
(i) f(x + 1) - f(x + 3) = 0
(ii) f(x + 3) + f(x) = 0
(iii) f(x-1) + f(x+3) = f(x+1) + f(x + 5)
(iv) f(x+p)=1+{(1−f(x−p))2n+1}12n+1,n∈N
View SolutionIf f'(x)=1−2sin2xf(x),(f(x)≥0,∀ξnRandf(0)=1) then f(x) is a periodic function with the period
View SolutionSuppose that f is an even, periodic function with period 2, and f(x)=x for all x in the interval [0,1]. The values of [10f(3.14)] is (where [.] represents the greatest integer function) ______
View SolutionSuppose that f is even, periodic function with period 2, and that f(x) = x for all x in the interval [0, 1]. Then draw the graph of y = f(x).
View SolutionAn even periodic function f:R→R with period 4 is such that
f(x)={max.(|x|,x2),0≤x<1x,1≤x≤2. Then draw the graph of y=f(x) for x∈R
View SolutionA function f is said to be periodic if it repeats its nature after certain interval and that interval is called period of the function. If T be the period of f(x), then f(x + T) = f(x). For example f(x) = tan x is periodic with period π. Then find the period of f(x) that satisfies the following condition.
(i) f(x + 1) - f(x + 3) = 0
(ii) f(x + 3) + f(x) = 0
(iii) f(x-1) + f(x+3) = f(x+1) + f(x + 5)
(iv) f(x+p)=1+{(1−f(x−p))2n+1}12n+1,n∈N
View Solution
