Suppose that two circles and in a plane have no points in common. Then
there is no line tangent to both and
there are exactly four lines tangent to both and
there are no lines tangent to both and or there are exactly two lines tangent to both and
there are no lines tangent to both and or there are exactly four lines tangent to both and
The correct Answer is:D
Since and in a plane have no points in common, either one circle is completely lying inside other without touching it or two circles are external without intersection or touching as shown in the following figure.
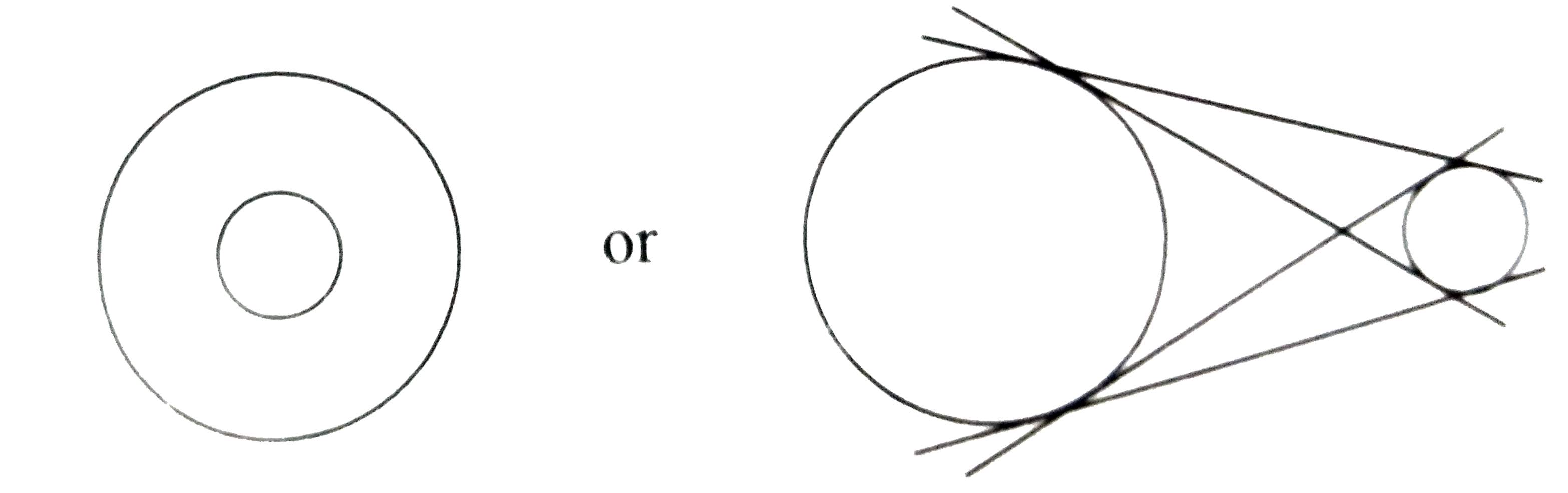
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
Similar Questions
Transverse common tangents are drawn from O to the two circles C1,C2 with 4, 2 respectively. Then the ratio of the areas of triangles formed by the tangents drawn from O to the circles C1andC2 and chord of contacts of O w.r.t the circles C1andC2 respectively is
View SolutionThe internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 are C1 Q are in
View Solution
Knowledge Check
If the two circles C1andC2 have three points in common, then which of the following is correct ?
AC1andC2 are concentricBC1andC2 are the same circleCC1andC2 have different centresDNone of the aboveThe centres of two circles C1andC2 each of unit radius are at a distance of 6 unit from each other. Let P be the mid-point of the line segment joining the centres of C1andC2 and C be a circle touching circles C1andC2 externally. If a common tangent to C1 and C passing through P is also a common tangent to C2 and C, then the radius of the circle C, is
A4B8C6D3Suppose we have two circles of radius 2 each in the plane such that the distance between their centres is 2√3. The area of the region common to both circles lies between
A0.5 and 0.6B0.65 and 0.7C0.7 and 0.75D0.8 and 0.9
Consider circles C1andC2 touching both the axes and passing through (4,4), then the x - intercept of the common chord of the circles is
View SolutionFrom a fixed point A three normals are drawn to the parabola y2=4ax at the points P, Q and R. Two circles C1 and C2 are drawn on AP and AQ as diameter. If slope of the common chord of the circles C1 and C2 be m1 and the slope of the tangent to teh parabola at R be m2, then m1×m2, is equal to
View SolutionA circle C1 has radius 2 units and a circles C2 has radius 3 units. The distance between the centres of C1 and C2 is 7 units. If two points, one tangent to both circles and the other passing through the centre of both circles, intersect at point P which lies between the centers of C1andC2, then the distance between P and the centre of C2 is
View SolutionLet C be a circle with centre P0andAB be a
diameter of C . suppose P1 is the midpoint of line
segment P0B,P2 the midpoint of line segment
P1B and so on Let C1,C2,C3 be circles with diameters P0P1,P1P2,P2P3 ,... respectively
Suppose the circles C1,C2,C2,... are all shaded
The ratio of the area of the unshaded portion of C
to that of the original circle is
View SolutionThe centres of two C1 and C2, each unit of unit radii, are at a distance of 6 units from each other. Let P be the mid-point of the line segment joining the centres of C1andC2. A third circle C is drawn such that it is externally tangent to both the circles C1andC2 at the same points where the lines passing through P are tangent to the circles C1andC2. The radius of the circle C is
View Solution
