The internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 are C1 Q are in
Step by step video & image solution for The internal common tangents to two circles with centre C_1 and C_2 intersect the line joining C_1 and C_2 at P and the two direct common tangents intersects the line joining C_1 and C_2 at Q. The length C_1P, C_1C_2 are C_1 Q are in by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 and C1 Q are in
View SolutionThe internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 are C1 Q are in
View Solution
Knowledge Check
The tangent to the curve y=ex drawn at the point (c,ec) intersects the line joining the points (c−1,ec−1) and (c+1,ec+1)
Aon the left of x=cBon the right of x=0Cat no pointDat all pointsThere are two circles C1 and C2 whose radii are r1,r2, respectively. If distance between their centre is 3r1−r2 and length of direct common tangent is twice of the length of transverse common tangent. Then r1:r2 is:
A5:4B6:5C7:6D8:7Let R1andR2 be the radil of the circles with centres at C1andC2.
Statement 1: If C1C2≤r1+r2, then the two circles have two common tangents. Because
Statemetn 2: For two common tangents the two circles must intersect in two points.AStateme-1 is True, Statement-2 is True, Statemetn-2 is correct explanation for Statement-1BStatement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1CStatement-1 is True, Statement-2 is FalseDStatement-1 is False, Statement-2 is ture
Let C1 be the circle of radius 1 with center at the origin. Let C2 be the circle of radius r with center at the point A=(4,1), where 1<r<3. Two distinct common tangents PQandST of C1 and C2 are drawn. The tangent PQ touches C1 at P and C2 at Q. The tangent ST touches C1 at S and C2 at T. Mid points of the line segments PQandST are joined to form a line which meets the x -axis at a point B . If AB=√5 , then the value of r2 is
View SolutionIn the figure given, two circles with centres Ct and C2 are 35 units apart, i.e. C1C2=35. The radii of the circles with centres C1 and C2 are 12 and 9 respectively. If P is the intersection of C1C2 and a common internal tangent to the circles, then l(C1P) equals
View SolutionCircles C1 and C2 are externally tangent and they are both internally tangent to the circle C_3. The radii of C1 and C2 are 4 and 10, respectively and the centres of the three circles are collinear. A chord of C3 is also a common internal tangent of C1 and C2. Given that the length of the chord is m√np where m,n and p are positive integers, m and p are relatively prime and n is not divisible by the square of any prime, find the value of (m+n+p).
View SolutionIn the given figure (not to scale), two circles C1andC2 intersect at S and Q. PQN and RQM are tangents drawn to C1andC2 respectively at Q. MAB and ABN are the chords of the circles C1andC2. If ∠NQR=85∘, then find ∠AQB.
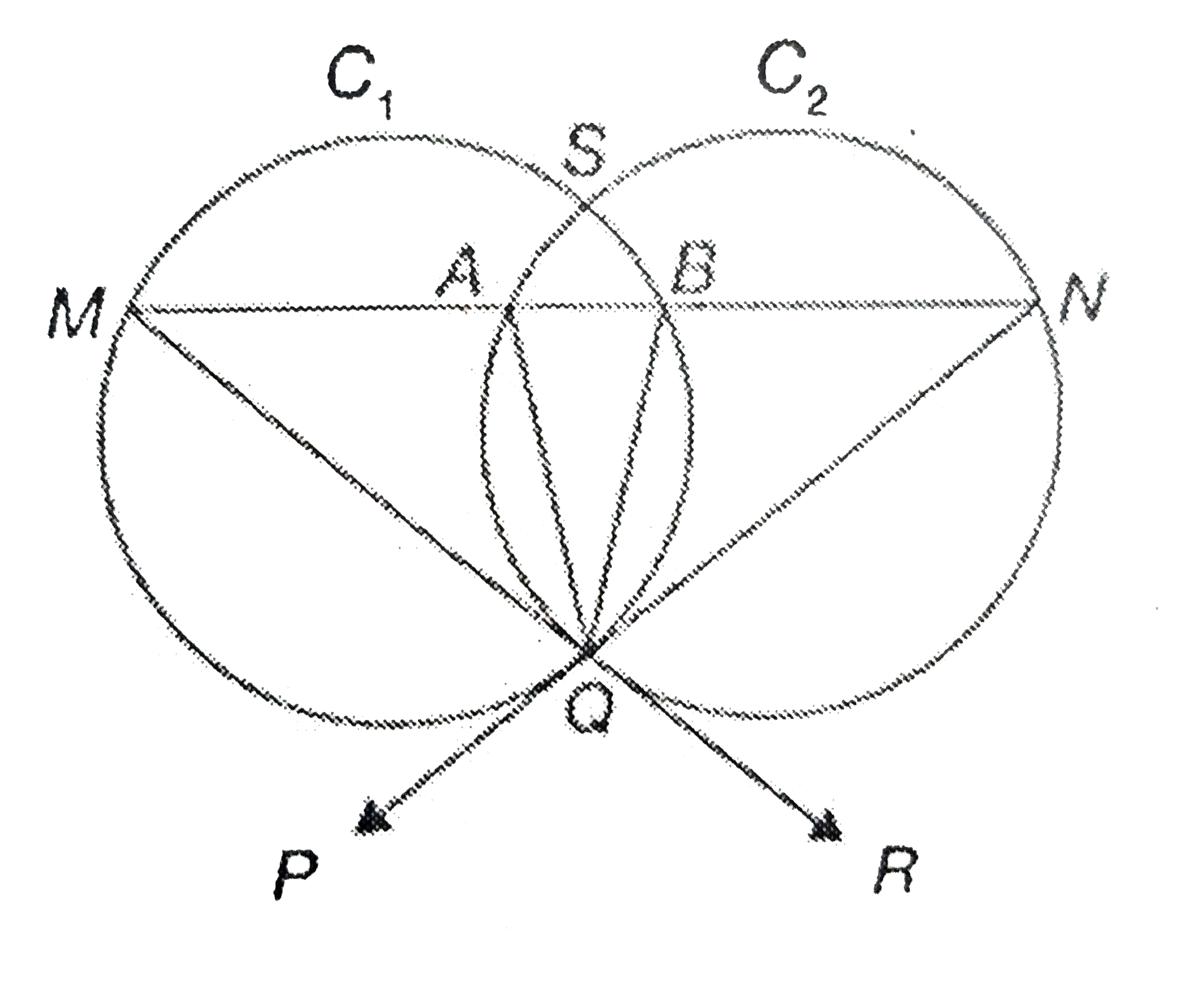
View SolutionAB is the common tangent to the circles C1 and C2. C1 and C2 are touching externally at C.AD and DC are two chords of the circle C1 and BE and CE are two chords of the circle C2. Find the measure of ∠ADC+∠BEC
View Solution
