Suppose the graph of f(x)=−x3 is translated 4 units right and 2 units down, resulting in the graph of a new function g. what is the value of g(-2)?
−218
−10
6
214
The correct Answer is:D
To solve the problem, we need to follow these steps:
Step 1: Understand the Translation
The function f(x)=−x3 is translated 4 units to the right and 2 units down. This means we need to adjust the function accordingly.
Step 2: Apply the Translation
1. Translation 4 units to the right: To translate a function f(x) to the right by a units, we replace x with x−a. Here, a=4, so we replace x with x−4.
f(x)→f(x−4)=−(x−4)3
2. Translation 2 units down: To translate a function down by b units, we subtract b from the function. Here, b=2, so we subtract 2 from the function:
g(x)=f(x−4)−2=−(x−4)3−2
Step 3: Write the New Function
Thus, the new function g(x) after the translations is:
g(x)=−(x−4)3−2
Step 4: Find g(−2)
Now we need to find the value of g(−2):
g(−2)=−((−2)−4)3−2
Calculating the expression inside the parentheses:
g(−2)=−(−6)3−2
Calculating (−6)3:
(−6)3=−216
Now substituting back into the equation:
g(−2)=−(−216)−2=216−2=214
Final Answer
Thus, the value of g(−2) is:
214
The function f(x)=−x3 is translated 4 units to the right and 2 units down. This means we need to adjust the function accordingly.
1. Translation 4 units to the right: To translate a function f(x) to the right by a units, we replace x with x−a. Here, a=4, so we replace x with x−4.
f(x)→f(x−4)=−(x−4)3
g(x)=f(x−4)−2=−(x−4)3−2
Thus, the new function g(x) after the translations is:
g(x)=−(x−4)3−2
Now we need to find the value of g(−2):
g(−2)=−((−2)−4)3−2
Calculating the expression inside the parentheses:
g(−2)=−(−6)3−2
Calculating (−6)3:
(−6)3=−216
Now substituting back into the equation:
g(−2)=−(−216)−2=216−2=214
Thus, the value of g(−2) is:
214
Topper's Solved these Questions
Similar Questions
Knowledge Check
Suppose the graph of f(x)=−x3+2 is translated 2 units right and 3 units down. If the result is the graph of Y=g(x), what is the value of g(-1.2)?
 A-33.77B-1.51C-0.49D31.77
A-33.77B-1.51C-0.49D31.77The graph og g(x)=x3+1 was translated 4 units to the right and 2 units up, resulting in a new graph h(x). What is the value of h(3.7) ?
A0.973B1.784C1.973D2.973Suppose the graph of f(x)=2x2 is translated 3 units down and 2 units right. If the resulting graph represents the graph of g(x), what is the value of g(−1.2) ?
A−1.72B−0.12C2.88D17.48
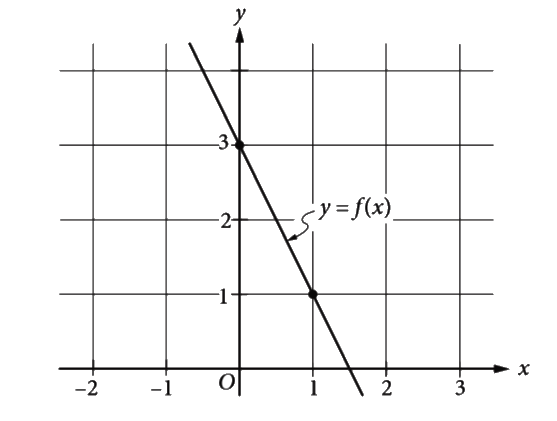
The graph of the linear function f is shown in the xy-plane above. The graph of the linear function g (not shown) is perpendicular to the graph of f and passes through the point (1,3). What is the value of g(0) ?
View Solution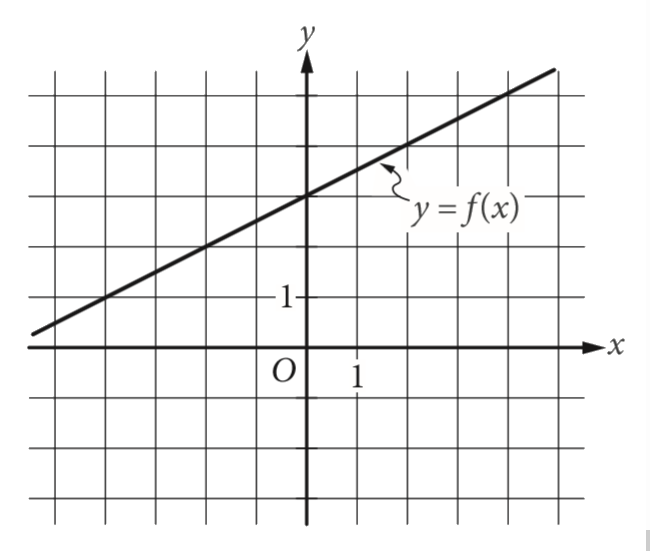
The graph of the linear functions f is shown in the xy-plane above. The slope of the graph of the linear function g is 4 times the slope of the graph of f. IF the graph of g passes through the point (0,-4) what is the value of g(9)?
View SolutionWhich of the following graphs is the graph of function g(x)|x−1|−1?
View SolutionFor the function f(x)=x2+2x−6, If the graph of f(x) is reflected across the x-axis , the graph of a new function, g(x) , is produced . Find g(3) .
View SolutionIf function g is defined by g(x)=x-1 and 2g(c)=10, what is the value of g(3c)?
View Solution
