Tangent drawn from the point P(4,0) to the circle x2+y2=8 touches it at the point A in the first quadrant. Find the coordinates of another point B on the circle such that AB=4 .
The correct Answer is:(2,−2) or (-2,2)
cosθ=2√24=1√2
θ=45∘
∴A≡(2,2)
Let B≡(x1,y1)
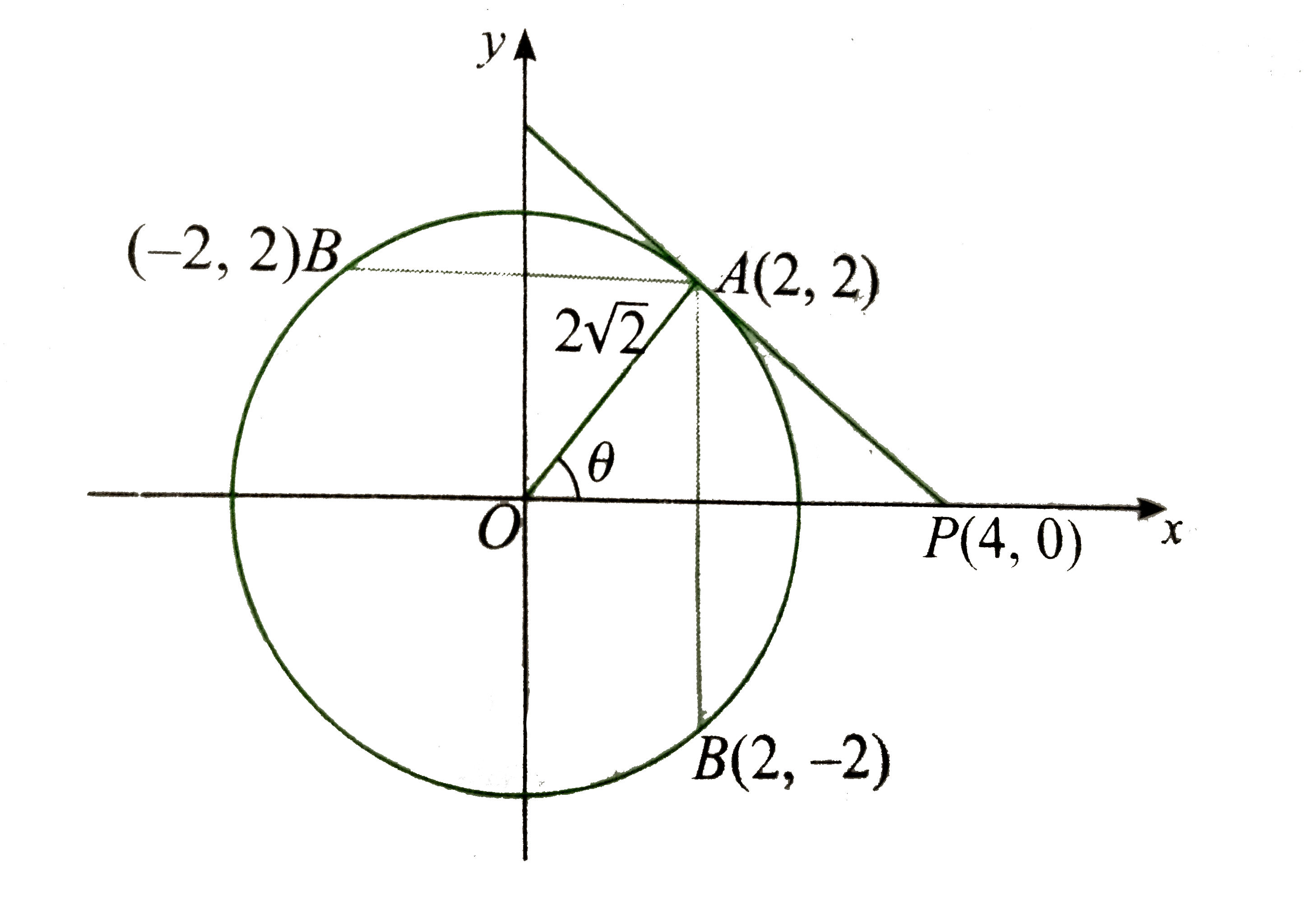
Given AB =4 . Therefore,
(x1−2)2+(y1−2)2=16
or x21+y21−4x1−4y1=8
Also, x21+y21=8
∴x1+y1=0
∴2x21=8
or x1±2
∴B≡(2,−2) or (−2,2)
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.8
5 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.9
5 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.6
6 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Tangents drawn from (2,0) to the circle x2+y2=1 touch the circle at AandB Then.
View SolutionTangents drawn from the point (4, 3) to the circle x2+y2−2x−4y=0 are inclined at an angle
View SolutionTangents are drawn from the point P(3,4) to the ellipse x29+y24=1 touching the ellipse at point A and B. Q. The coordinates of A and B are
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A&B ifR is the radius of circum circle of triangle PAB then [R]-
View SolutionTangents are drawn from the point P(3,4) to the ellipse x29+y24=1 touching the ellipse at point A and B. Q. The orthocenter of the trianlge PAB is
View SolutionTo the circle x2+y2+8x−4y+4=0 tangent at the point θ=π4 is
View SolutionThe point of contact of a tangent from the point (1,2) to the circle x2+y2=1 has the coordinates :
View SolutionTangents are drawn from the points on the line x−y−5=0 to x2+4y2=4 . Then all the chords of contact pass through a fixed point. Find the coordinates.
View SolutionTangents are drawn from the point P(1,−1) to the circle x2+y2−4x−6y−3=0 with centre C, A and B are the points of contact. Which of the following are correct?
View SolutionTangents drawn from P(1,8) to the circle x2+y2−6x−4y−11=0 touches the circle at the points A and B, respectively. The radius of the circle which passes through the points of intersection of circles x2+y2−2x−6y+6=0andx2+y2−2x−6y+6=0 the circumcircle of the and interse ΔPAB orthogonally is equal to
View Solution
