Tangent drawn from the point P(4,0) to the circle x2+y2=8 touches it at the point A in the first quadrant. Find the coordinates of another point B on the circle such that AB=4 .
The correct Answer is:(2,−2) or (-2,2)
cosθ=2√24=1√2
θ=45∘
∴A≡(2,2)
Let B≡(x1,y1)
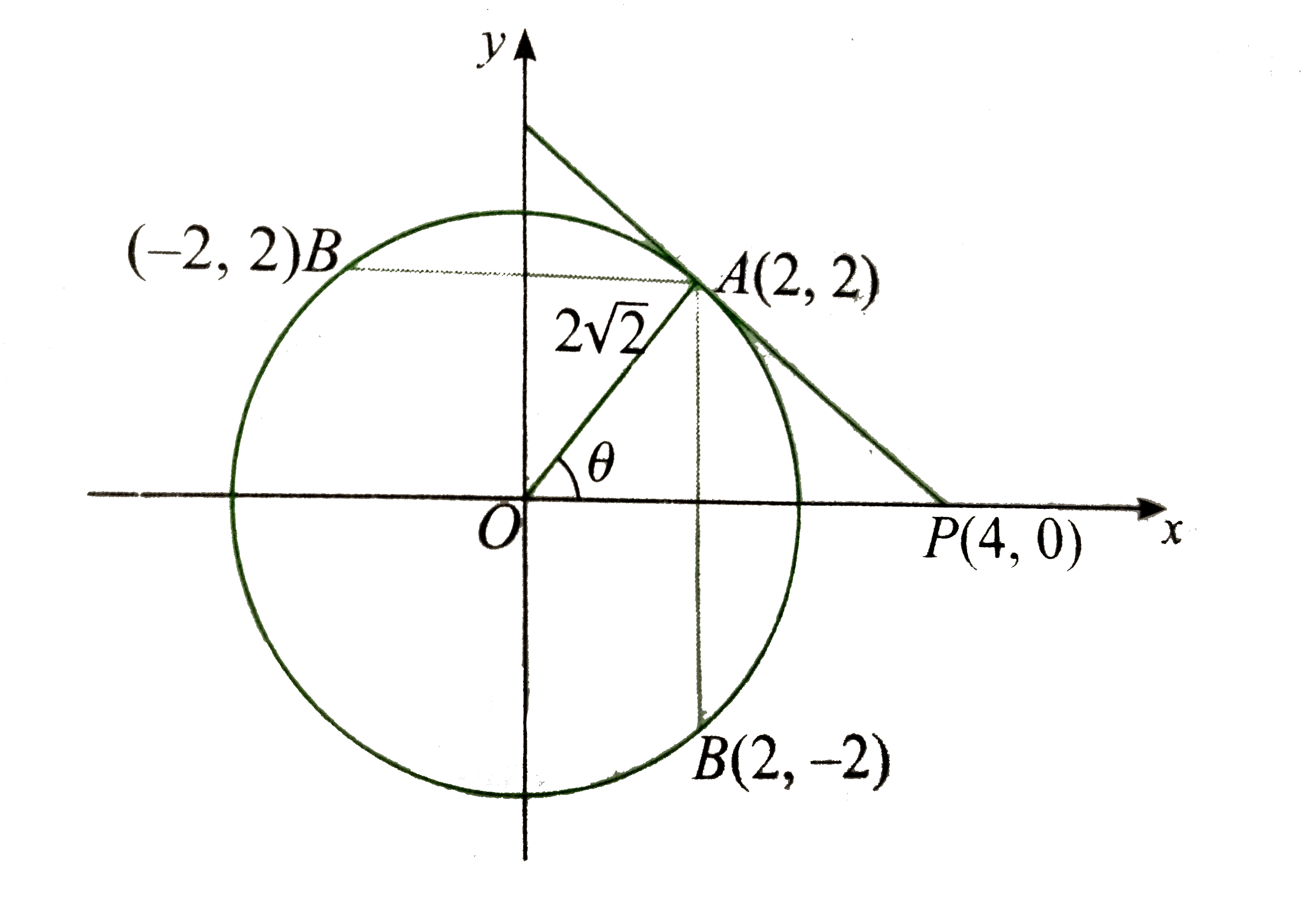
Given AB =4 . Therefore,
(x1−2)2+(y1−2)2=16
or x21+y21−4x1−4y1=8
Also, x21+y21=8
∴x1+y1=0
∴2x21=8
or x1±2
∴B≡(2,−2) or (−2,2)
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.85videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.95videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.66videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
Tangent drawn from the point P(4,0) to the circle x2+y2=8 touches it at the point A in the first quadrant. Find the coordinates of another point B on the circle such that AB=4 .
View SolutionTangents are drawn from the point P(3,4) to the ellipse x29+y24=1 touching the ellipse at point A and B. Q. The coordinates of A and B are
View Solution
Knowledge Check
- Question 1 - Select One
Tangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B the equation of the circumcircle of △PAB is
Ax2+y2÷4x−6y+19=0Bx2+y2−4x−10y+19=0Cx2+y2−2x+6y−29=0Dx2+y2−6x−4y+19=0 - Question 2 - Select One
Tangents are drawn from the point P(3,4) to the ellipse x29+y24=1 touching the ellipse at point A and B. Q. The coordinates of A and B are
A(3,0) amd (0,2)B(−85,(2√16115)and(−98,85)C(−85,(2√16115)and(0,2)D(3,0)and(−95,85) - Question 3 - Select One
Tangents drawn from the point P (1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is
Ax2+y2+4x−6y+19=0Bx2+y2−4x−10y+19=0Cx2+y2−2x+6y−20Dx2+y2−6x−4y+19=0
Tangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A&B ifR is the radius of circum circle of triangle PAB then [R]-
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A&B ifR is the radius of circum circle of triangle PAB then [R]-
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View Solution