Tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Find length of PQ
Given,
Radius {OP}=5 {cm} and {OQ}=12 {cm}
{PQ} is the tangent to the circle.
angle O P Q=90∘
Therefore ,by Pythagoras theorem we get,
PQ2=OQ2−OP2
⇒P2=122−52
⇒PQ2=144−25
⇒PQ2=119
⇒PQ=√119{cm}
Topper's Solved these Questions
Similar Questions
Tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Find length of PQ
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ=13cm . Find the length of PQ .
View Solution
Knowledge Check
A tangent PQ at a point P of a circle of radius 5cm meets a line through the centre O at a point Q so that OQ=13cm. Find the length of PQ.
A12 cmB7 cmC10 cmD15 cmA tangent PQ at point P of a circle of radius 12 cm meets a line through the centre O to a point Q so that OQ = 20 cm . Length PQ is :
A14B15C16D10A tangent AB at a point A of a circle of radius 5 cm meets a line through the centre O at a point B so that OB = 12 cm , Length AB is
A10 cmB12 cmC9 cmD√119 cm
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ =12 cm . Length PQ is :
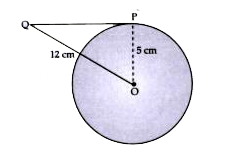
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is:
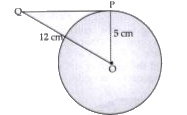
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ=12 cm. Length PQ is :
(A) 12 cm (B) 13 cm (C) 8.5 cm (D) √119cm.
View SolutionA tangent PQ at a point P of a circle of radius 5cm meets a line through the centre O at a point Q such that OQ=12cm . Length PQ is (a) 12cm (b) 13cm (c) 8.5cm (d) √119cm
View SolutionA tangent AB, at a point A of a circle of radius 5 cm, meets a line through the centre O at point B such that OB =12 cm. Length AB is
View Solution
