Tangents are drawn to the circle x2+y2=a2 from two points on the axis of x, equidistant from the point (k,0). Show that the locus of their intersection is ky2=a2(k−x).
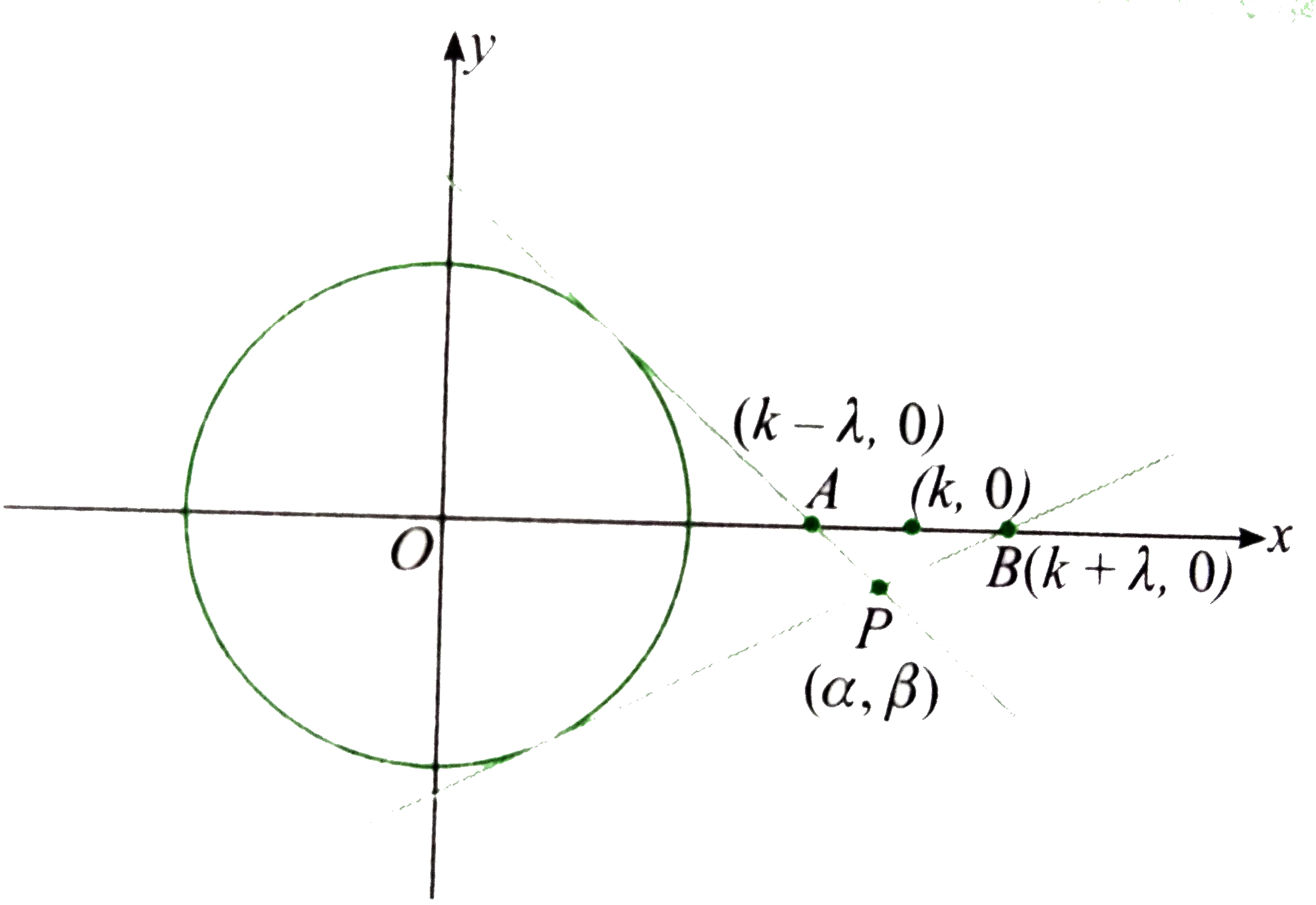
As shown in figure , point A and B are equidistant from point (k,0).
Tangents drawn from point A and B intersect at point P(α,β).
Equation of pair of tangents from point P is
(x2+y2−a2)(α2+β2−a2)=(αx+βy−a2)2 (Using T2=SS1)
This equation is satisfied by points A and B .
∴((k−λ)2−a2)(α2+β2−a2)=(α(k−λ)−a2)2 (1)
and ((k+λ)2−a2)(α2+β2−a2)=(α(k+λ)−a2)2 (2)
Subtracting (1) and (2) , we get
(α2+β2−a2)(4kλ)=[(k+λ)α−a2+(k−λ)α−a2][(k+λ)α−(k−λ)α]=[2(kα−a2)][2λα]=4λα[kα−a2]
⇒k(α2+β2−a2)=kα2−a2α
⇒kβ2=a2(k−α)
Hence, the locu is ky2=a2(k−x)
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.1
1 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.2
2 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
7 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Tangents are drawn to the hyperbola 3x2−2y2=25 from the point (0,52). Find their equations.
View SolutionTangents are drawn to the hyperbola 3x2−2y2=25 from the point (0,52). Find their equations.
View SolutionFind the locus of a point equidistant from the point (2,4) and the y-axis.
View SolutionFind the locus of a point equidistant from the point (2,4) and the y-axis.
View SolutionIf the points (2, 1) and (1, −2) are equidistant from the point (x, y) , show that x+3y=0 .
View SolutionTangents are drawn to the circle x2+y2=16 at the points where it intersects the circle x2+y2−6x−8y−8=0, then the point of intersection of these tangents is
View SolutionFind the value of k , if the point P (2,4) is equidistant from the points A(5,k) and B(k,7).
View SolutionFind the value of k , if the point P (2,4) is equidistant from the points A(5,k) and B(k,7).
View SolutionTangents are drawn to the circle x2+y2=9 at the points where it is met by the circle x2+y2+3x+4y+2=0 . Find the point of intersection of these tangents.
View SolutionTangents are drawn to the circle x2+y2=12 at the points where it is met by the circle x2+y2−5x+3y−2=0 . Find the point of intersection of these tangents.
View Solution
