Question

Tangents are drawn to the ellipse ${\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1,(a>b),}$
and the circle ${\displaystyle x^2+y^2=a^2}$
at the points where a common ordinate cuts them (on the same side of the
x-axis). Then the greatest acute angle between these tangents is given by
${\displaystyle {\tan }^{-1}\left(\frac{a-b}{2\sqrt{ab}}\right)}$
(b) ${\displaystyle {\tan }^{-1}\left(\frac{a+b}{2\sqrt{ab}}\right)}$

${\displaystyle {\tan }^{-1}\left(\frac{2ab}{\sqrt{a-b}}\right)}$
(d) ${\displaystyle {\tan }^{-1}\left(\frac{2ab}{\sqrt{a+b}}\right)}$

Options

A. `tan^(-1)((a-b)/(2sqrt(ab)))`
B. `tan^(-1)((a+b)/(2sqrt(ab)))`
C. `tan^(-1)((2ab)/(2sqrt(a-b)))`
D. `tan^(-1)((2ab)/(2sqrt(a+b)))`

Explanation

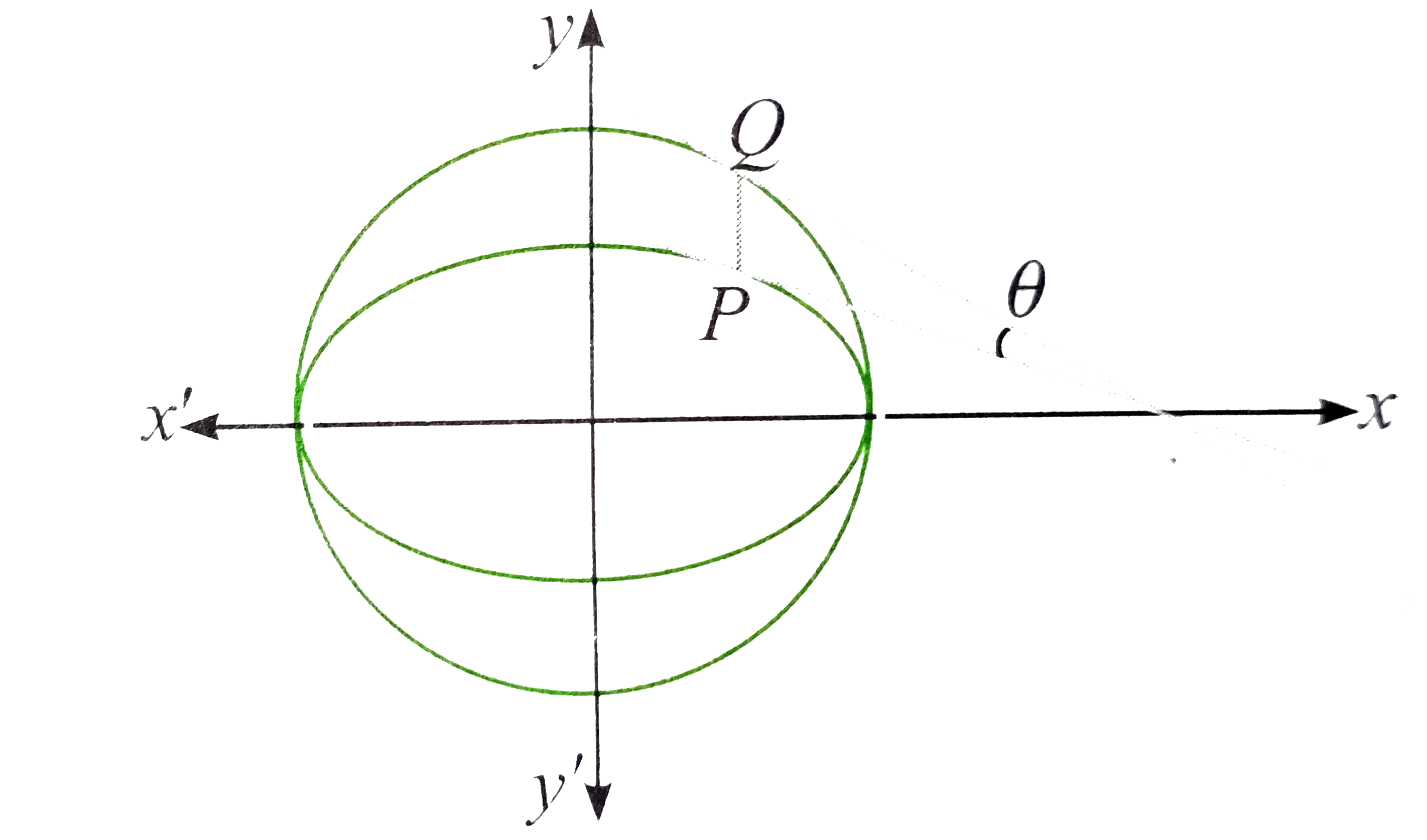
Tanent to the ellipse at `P( a cos alpha, b sin alpha)` is `(x)/(a) cos alpha+(y)/(b) isn alpha=1" "(1)`
Tangent to the circle at `Q(a cos, alpha, a sin alpha)` is ` cos ax+sin alphay=a " "(2)`
Now, the angle between the tangents is `theta`. Then, `tan theta=|(-(b)/(a)cotalpha-(-cot alpha))/(1+(-(b)/(a)cot alpha)(-cot alpha))|`
`=|(cos alpha(1-(b)/(a)))/(1+(b)/(a)cot^(2)alpha)|=|(a-b)/(a tan alpha+b cot alpha)|`
`=|(a-b)/((sqrt(atanalpha)-sqrt(bcotalpha))^(2)+2sqrt(ab))|`
Now, the greatest value of the above expression is `|(a-b)/(2sqrt(ab))|` when `sqrt(tan alpha)= sqrt (b tan alpha)`. Therefore,
`theta_("maximum")=tan^(-1)((a-b)/(2sqrt(ab)))`