Tangents PA and PB are drawn to the circle (x−4)2+(y−5)2=4 from the point P on the curvey=sinx , where A and B lie on the circle. Consider the function y=f(x) represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
Which of the following is true ?
2π
3π
π
not defined
The correct Answer is:3
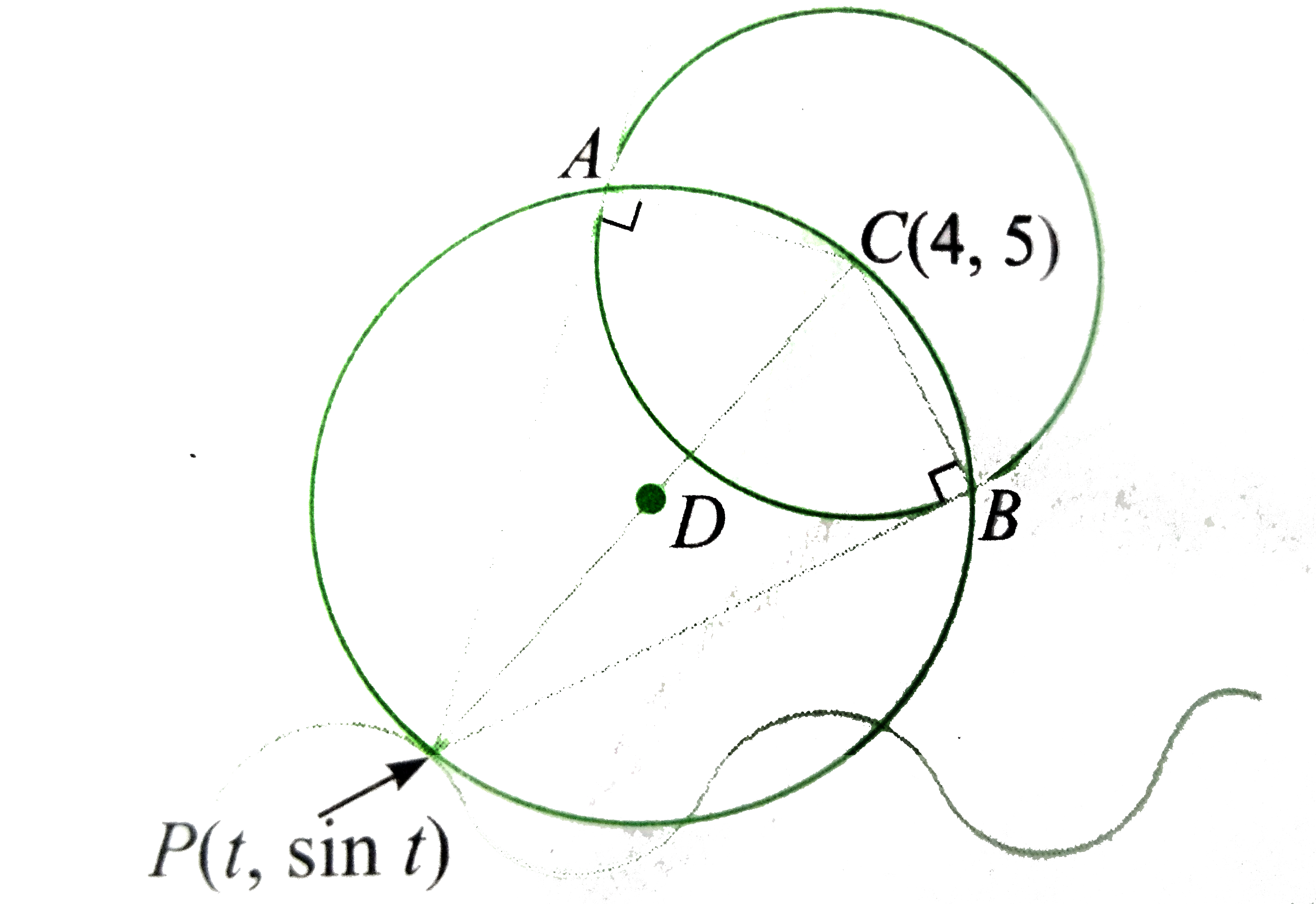
The center of the given circle is C(4,5) . Points P,A,C, and B are concyclic such that PC is the diameter of the circle. Hence, the center D(h,k) of the circumcircle of ΔABC is the midpoint of PC.
Then, we have
h=t+42 and k=sint+52
Eliminating t, we have
k=sin(2h−4)+52
or y=f(x)=sin(2x−4)+52
∴f−1(x)=sin−1(2x−5)+42
Thus, the range of
y=sin(2x−4)+52
is [2,3] and the priod is π.
Al,so f(x)=4, i.e.., sin(2x−4)=3 which has no real solutions.
For f(x)=1,sin(2x−4)=3 which has no real solutions.
But range of y=sin−1(2x−5)+42 is [−π3+2,π4+2]
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
7 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - NUMERICAL VALUE TYPE
21 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Linked Comprehension Type Based upon each paragraph, three multiple choice questions have to be answered. Each question has four choices: a, b, c, and d, out of which only one is correct For Problems 1-3 center is at Each side of a square has length 4 units and its (3, 4). If one of the diagonals is parallel to the line y x, then answer the following questions 1. Which of the following is not the vertex of the square? a. (1, 6) b. (5, 2) c. (1, 2) d. (4, 6) 2. The radius of the circle inscribed in the triangle formed by any three vertices is a. 2020V2 1) 2012 1) d. none of these 3. The circle inscribed in the triangle forme radius of the by any two vertices of the square and the center is b. 202 1) a. 2012 1) d. none of these v2012 1) For Problems 4-6 Tangents PA and PB are drawn to the circle (x 4) 4 from the point P on the curve y sin x, where A and B on the circle. Consider the function y f(r) represented by locus of the center of the circumcircle of triangle PAB. T answer the following questions
View SolutionTangents PA and PB are drawn to the circle (x+3)2+(y−4)2=1 from a variable point P on y=sinx. Find the locus of the centre of the circle circumscribing triangle PAB.
View Solution
Knowledge Check
Tangents PA and PB are drawn to the circle (x−4)2+(y−5)2=4 from the point P on the curvey=sinx , where A and B lie on the circle. Consider the function y=f(x) represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
The range of y=f(x) isA[−2,1]B[−1,4]C[0,2]D[2,3]Tangents PA and PB are drawn to the circle (x−4)2+(y−5)2=4 from the point P on the curvey=sinx , where A and B lie on the circle. Consider the function y=f(x) represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
The period of y=f(x) isA2πB3πCπDnot definedTangents PA and PB are drawn to x2+y2=4 from the point P(3,0). Area of triangle PAB is equal to:-
A109√5 sq. unitsB203√5 sq. unitsC59√5 sq. unitsDNone of these
Tangents PA and PB are drawn to the ellipse x216+y29=1 from the point P(0, 5). Area of triangle PAB is equal to
View SolutionTangents PA and PB are drawn to the circle x2+y2=4,then locus of the point P if PAB is an equilateral triangle ,is equal to
View SolutionTangents PA and PB are drawn to x2+y2=4 from the point P(3,0). Area of triangle PAB is equal to:-
View SolutionTangents PAandPB are drawn to the circle x2+y2=8 from any arbitrary point P on the line x+y=4. The locus of mid-point of chord of contact AB is
View SolutionTangents PA and PB are drown to the circle S=x2+y2−2y−3=0 from the point P (3,4). which of the following altematives (s) is/are correct ?
View Solution
