Tell whether a figure’s surface area has increased or decreased if each dimension of the figure is changed by a factor of13.
To determine whether a figure's surface area has increased or decreased when each dimension of the figure is changed by a factor of 13, we can follow these steps:
1. Understand the Original Dimensions:
Let the original dimensions of the cuboid be:
- Length = L
- Breadth = B
- Height = H
2. Calculate the Original Surface Area:
The formula for the total surface area (SA) of a cuboid is given by:
SA=2(LB+BH+HL)
Substituting the original dimensions, we have:
SAoriginal=2(LB+BH+HL)
3. Change Each Dimension by a Factor of 13:
After changing each dimension, the new dimensions will be:
- New Length = L3
- New Breadth = B3
- New Height = H3
4. Calculate the New Surface Area:
Using the new dimensions, the new surface area can be calculated as:
SAnew=2(L3⋅B3+B3⋅H3+H3⋅L3)
Simplifying this gives:
SAnew=2(LB9+BH9+HL9)=2⋅19(LB+BH+HL)=29(LB+BH+HL)
5. Compare the Original and New Surface Areas:
Now we can compare the original surface area with the new surface area:
- Original Surface Area: SAoriginal=2(LB+BH+HL)
- New Surface Area: SAnew=29(LB+BH+HL)
6. Determine the Change in Surface Area:
To see if the surface area has increased or decreased, we can express the ratio of the new surface area to the original surface area:
Ratio=SAnewSAoriginal=29(LB+BH+HL)2(LB+BH+HL)=19
Since 19<1, this indicates that the new surface area is less than the original surface area.
Conclusion:
The surface area of the figure has decreased when each dimension is changed by a factor of 13.
Let the original dimensions of the cuboid be:
- Length = L
- Breadth = B
- Height = H
The formula for the total surface area (SA) of a cuboid is given by:
SA=2(LB+BH+HL)
Substituting the original dimensions, we have:
SAoriginal=2(LB+BH+HL)
After changing each dimension, the new dimensions will be:
- New Length = L3
- New Breadth = B3
- New Height = H3
Using the new dimensions, the new surface area can be calculated as:
SAnew=2(L3⋅B3+B3⋅H3+H3⋅L3)
Simplifying this gives:
SAnew=2(LB9+BH9+HL9)=2⋅19(LB+BH+HL)=29(LB+BH+HL)
Now we can compare the original surface area with the new surface area:
- Original Surface Area: SAoriginal=2(LB+BH+HL)
- New Surface Area: SAnew=29(LB+BH+HL)
To see if the surface area has increased or decreased, we can express the ratio of the new surface area to the original surface area:
Ratio=SAnewSAoriginal=29(LB+BH+HL)2(LB+BH+HL)=19
Since 19<1, this indicates that the new surface area is less than the original surface area.
The surface area of the figure has decreased when each dimension is changed by a factor of 13.
Topper's Solved these Questions
- VISUALISING SOLID SHAPES BOOK - NCERT EXEMPLARCHAPTER - VISUALISING SOLID SHAPES EXERCISE - EXERCISE
91 Videos
- VISUALISING SOLID SHAPES BOOK - NCERT EXEMPLARCHAPTER - VISUALISING SOLID SHAPES EXERCISE - TRY THIS
5 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
Similar Questions
Knowledge Check
If each side of a cube is decreased by 19%, then decrease in surface area is
A0.4B0.384C0.35D0.3439
Find the surface area and the volume of a beach ball shown in the figure.
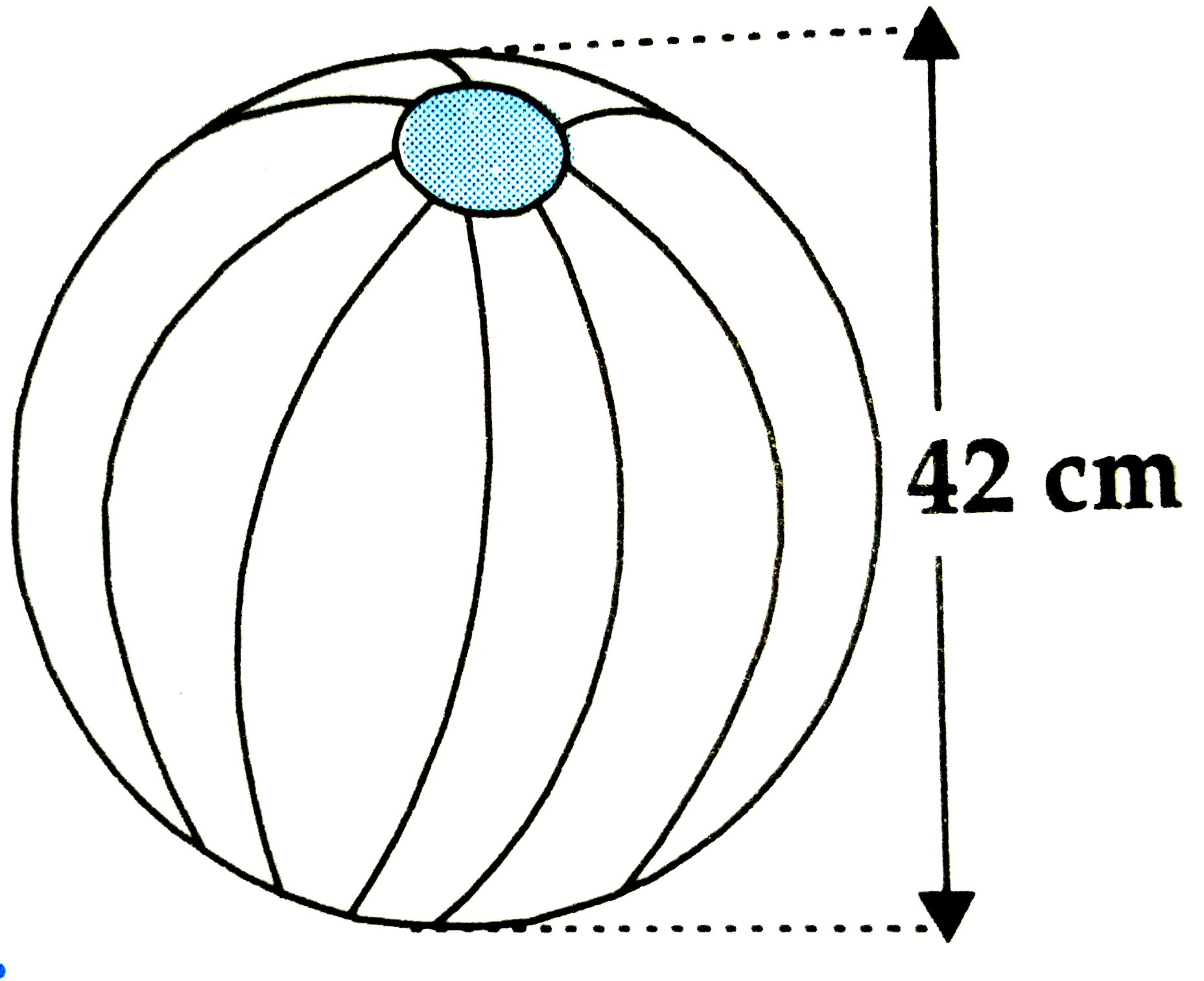
View SolutionFind the surface area and the volume of a beach ball shown in the figure.
View SolutionExplain how the volume of a figure is changed if each dimension is multiplied by a factor of 2.
View SolutionFind the surface area and volume of a beach ball shown in the figure
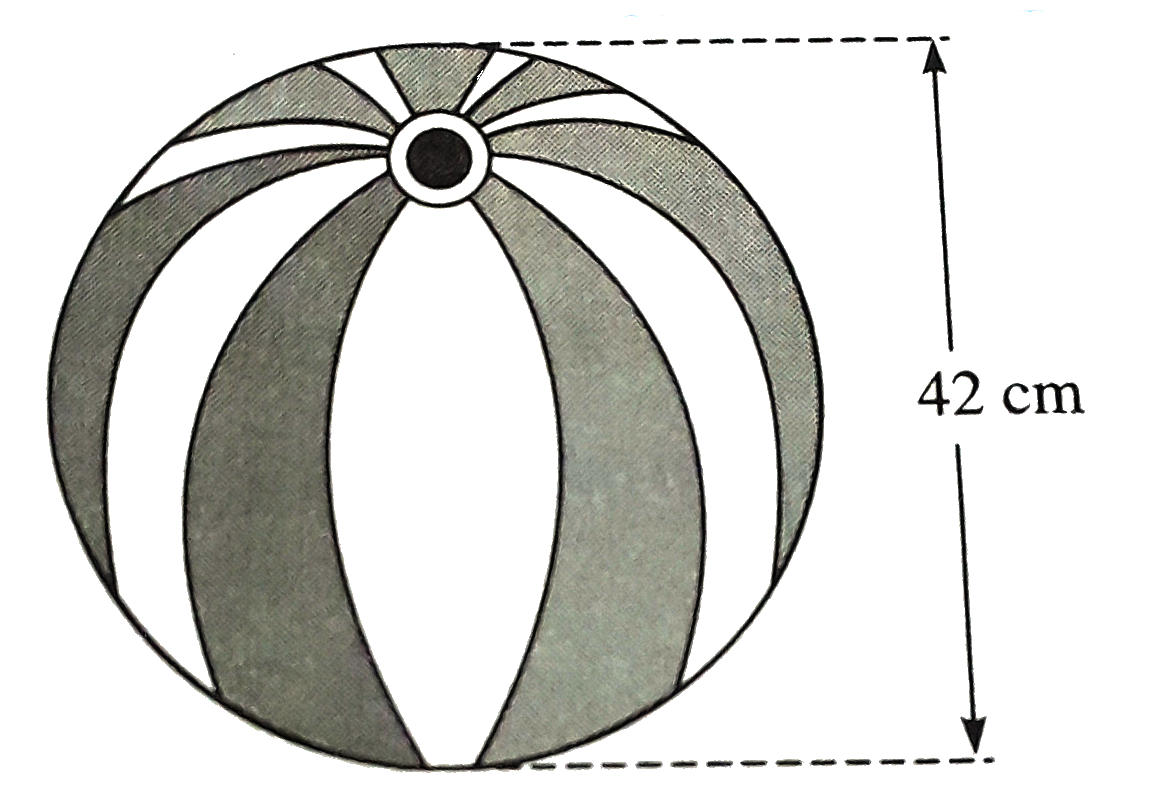
View Solution

Tell whether each figure has rotational symmetry. Write yes or no.
View SolutionAn increase in perimeter of a figure always increases the area of the figure.
View SolutionTo increase pressure, either force has to be in increased or area of contact has to be decreased.
View Solution