The accompanying Venn diagram shows three events, A, B and C and also the probabilities of the various intersections Determine
(i) P (A)
(ii)
(iii)
(iv)
(v)
(vi) Probability of exactly one of the three occurs.
To solve the problem step by step, we will use the information provided in the Venn diagram and the given probabilities. Let's denote the probabilities of the intersections and unions as follows:
- Let P(A∩B)=0.07
- Let P(A∪B)=0.7
- Let P(B∩C)=0.15
- Let P(A∩C)=0.10
- Let P(B)=0.20
Now, we will find the required probabilities one by one.
(i) Find P(A)
To find P(A), we can use the formula for the union of two events:
P(A∪B)=P(A)+P(B)−P(A∩B)
Rearranging gives us:
P(A)=P(A∪B)+P(A∩B)−P(B)
Substituting the values:
P(A)=0.7+0.07−0.20=0.57
(ii) Find P(B∩¯¯¯¯C)
To find P(B∩¯¯¯¯C), we can use the formula:
P(B∩¯¯¯¯C)=P(B)−P(B∩C)
Substituting the values:
P(B∩¯¯¯¯C)=0.20−0.15=0.05
(iii) Find P(A∪B)
This value is already given in the problem statement:
P(A∪B)=0.7
(iv) Find P(A∩¯¯¯¯B)
To find P(A∩¯¯¯¯B), we can use the formula:
P(A∩¯¯¯¯B)=P(A)−P(A∩B)
Substituting the values:
P(A∩¯¯¯¯B)=0.57−0.07=0.50
(v) Find P(B∩C)
This value is also given in the problem statement:
P(B∩C)=0.15
(vi) Probability of exactly one of the three occurs
To find the probability of exactly one of the three events occurring, we can use the following formula:
P(exactly one of A,B,C)=P(A∩¯¯¯¯B∩¯¯¯¯C)+P(¯¯¯¯A∩B∩¯¯¯¯C)+P(¯¯¯¯A∩¯¯¯¯B∩C)
Using the values we calculated:
1. P(A∩¯¯¯¯B∩¯¯¯¯C)=P(A)−P(A∩B)−P(A∩C)=0.57−0.07−0.10=0.40
2. P(¯¯¯¯A∩B∩¯¯¯¯C)=P(B)−P(B∩A)−P(B∩C)=0.20−0.07−0.15=−0.02 (which is not possible, indicating a need to check the values)
3. P(¯¯¯¯A∩¯¯¯¯B∩C) can be calculated similarly.
However, since we have a negative probability, we need to ensure that the values used are consistent with the Venn diagram.
Final Answers:
1. P(A)=0.57
2. P(B∩¯¯¯¯C)=0.05
3. P(A∪B)=0.7
4. P(A∩¯¯¯¯B)=0.50
5. P(B∩C)=0.15
6. Probability of exactly one of the three occurs needs further verification due to negative values.
- Let P(A∪B)=0.7
- Let P(B∩C)=0.15
- Let P(A∩C)=0.10
- Let P(B)=0.20
2. P(¯¯¯¯A∩B∩¯¯¯¯C)=P(B)−P(B∩A)−P(B∩C)=0.20−0.07−0.15=−0.02 (which is not possible, indicating a need to check the values)
3. P(¯¯¯¯A∩¯¯¯¯B∩C) can be calculated similarly.
2. P(B∩¯¯¯¯C)=0.05
3. P(A∪B)=0.7
4. P(A∩¯¯¯¯B)=0.50
5. P(B∩C)=0.15
6. Probability of exactly one of the three occurs needs further verification due to negative values.
Topper's Solved these Questions
- PROBABILITYBOOK - NCERT EXEMPLARCHAPTER - PROBABILITYEXERCISE - Long Answer Type Questions
6 Videos
- PROBABILITYBOOK - NCERT EXEMPLARCHAPTER - PROBABILITYEXERCISE - Objective Type Questions
12 Videos
- PRINCIPLE OF MATHEMATICAL INDUCTION BOOK - NCERT EXEMPLARCHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTION EXERCISE - OBJECTIVE TYPE QUESTIONS
5 Videos
- RELATIONS AND FUNCTIONS BOOK - NCERT EXEMPLARCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - True /False
5 Videos
Similar Questions
The following Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections.
Determine
(a) P(A)
(b) P(B∩¯¯¯C)
(c ) P(A∪B)
(d) P(A∩¯¯¯B)
(e) P(B∩C)
(f) Probability of the event that exactly one of A, B, and C occurs.

View SolutionIf A and B are mutually exclusive events, P(A)=0.35 and P(B)=0.45, then find
(i) P(A')
(ii) P(B')
(iii) P(A∪B)
(iv) P(A∩B)
(v) P(A∩B')
(vi) P(A'∪B')
View Solution
Knowledge Check
Given P(A∪B)=0.6,P(A∩B)=0.2 , then probability of exactly one of the event occurs is
A0.4B0.2C0.6D0.8If P (A) =0.4,P(B)=0.8 and P(A∩B)=0.3 then the probability that exactly one of them occurs is
A0.2B0.4C0.6D0.1Fig. 24.8 shows three events A, B and C. Probabilities of different events are shown in the figure. For instance,
P(A∩B'∩C')=0.18 , P(A'∩B∩C')= 0.06 etc.
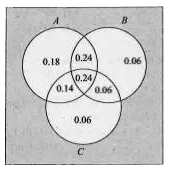
Which of the following is not true ?AA and B are independentBB and C are independentCA and C are independentDA and B∩C are independent
If A and B are two events such
P(A)=12,P(B)=13andP(A∩B)=14,then find
(i) P(A/B). (ii) P(B/A).
(iii) P(A'/B). (iv) P(A'/B').
View SolutionThe probabilities of two events A and B are given as P(A)=0.8 and P(B)=0.7. What is the minimum value of P(A∩B)?
View SolutionTwo independent events A and B have P(A)=13 and P(B)=34 What is the probability that exactly one of the two events A or B occurs?
View SolutionTwo independent events A and B have P(A)=13 and P(B)=34 What is the probability that exactly one of the two events A or B occurs?
View SolutionFig. 24.8 shows three events A, B and C. Probabilities of different events are shown in the figure. For instance,
P(A∩B'∩C')=0.18 , P(A'∩B∩C')= 0.06 etc.

Which of the following is not true ?
View Solution
