The angle biosectors BD and CE of a triangle ABC are divied by the incentre 1 in the rartios 3 : 2 and 2 : 1 respecticely. Then the ratio in which I divides the bisector through A is-
A
3:1
B
11:4
C
6:5
D
7:4
Video Solution
Text Solution
The correct Answer is:B
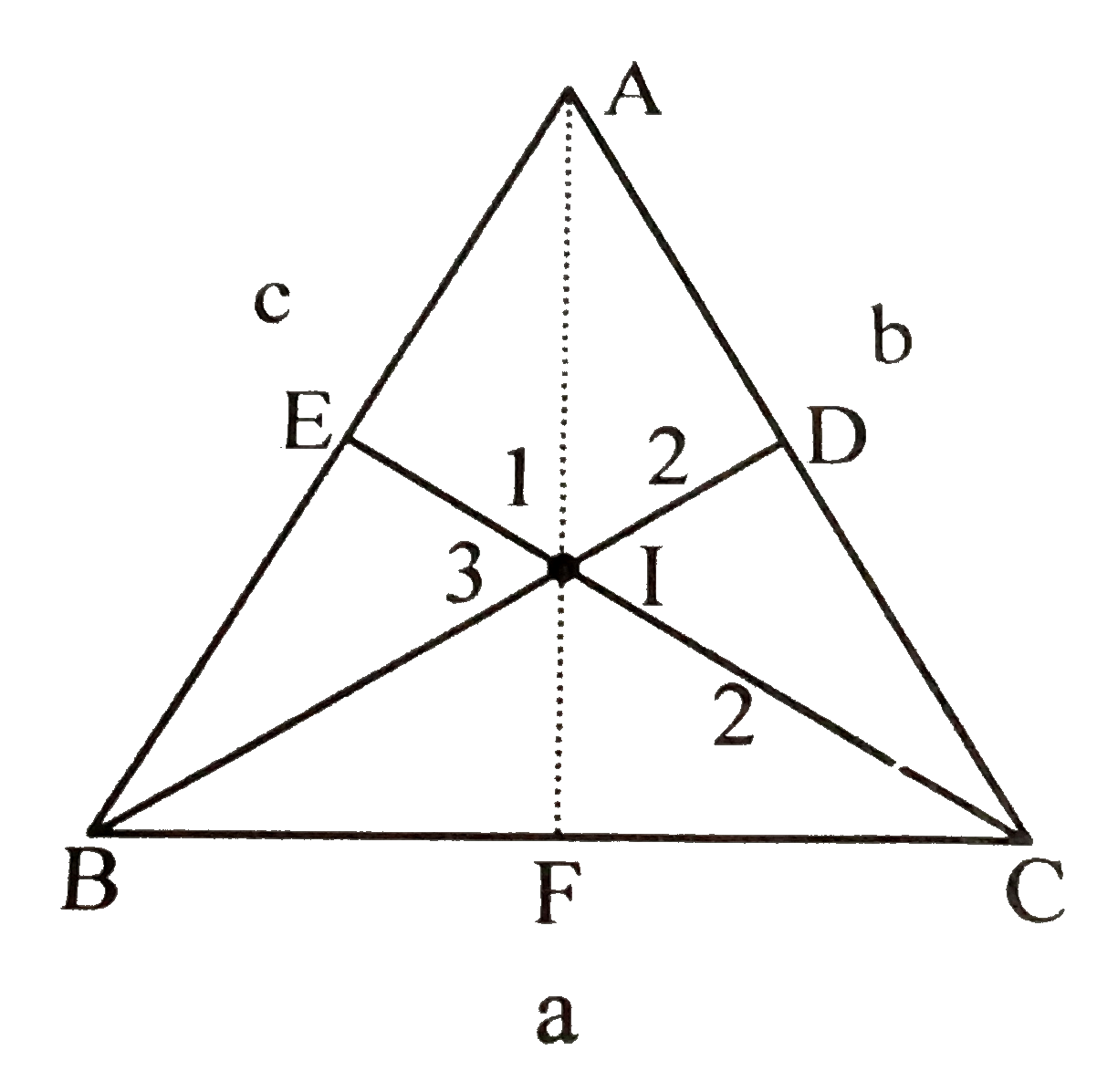
I divides AF
b + c : a
I divides BD
c + a : b
I divides CE in
a + b : c
c+ab=32,a+bc=21
2c+2a=3b⇒a+b+=2c⇒a+b+2a=3b a+3a2=2c⇒3a=2b 52a=2c⇒b=3a2 c=54a
Now b+ca=3a2+5a4a=6+54=114
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the angles of a triangle ABC are in the ratio 2:3:1 then the angles A,B and C are
A∠A=60∘,an≥lB=90∘∘,∠C=30∘B∠A=40∘,an≥lB=120∘∘,∠C=20∘C∠A=20∘,an≥lB=60∘∘,∠C=60∘D∠A=45∘,an≥lB=90∘∘,∠C=45∘The angles of a triangle ABC are in the ratio 3:5:4 then a+b+c√2=
A2bB3bC2cD3aIf the sides of triangle ABC are such that a=4b=5,c=6, then the ratio in which incentre divide the angle bisector of B is
A2:3B2:1C5:2D1:1
The angles of a triangle are in the ratio 3 : 4 : 5. If l be the incentre of ΔABC then find the measure of ∠ADC where AD, is the bisector of ∠A.
View SolutionIf the angles of a triangle ABC are in the ratio 2 : 3 : 1, then the angles, ∠A,∠Band∠C are
View SolutionThe angles of a triangle are in the ratio 1:2:3 , then the sides of a triangle are in the ratio
View SolutionIf the angles of a triangle ABC are in the ratio 1:2:3. then the corresponding sides are in the ratio ?
View SolutionIf the angles of a triangle ABC are in the ratio 2 : 3 : 1, then the angles, ∠A,∠Band∠C are
View Solution
