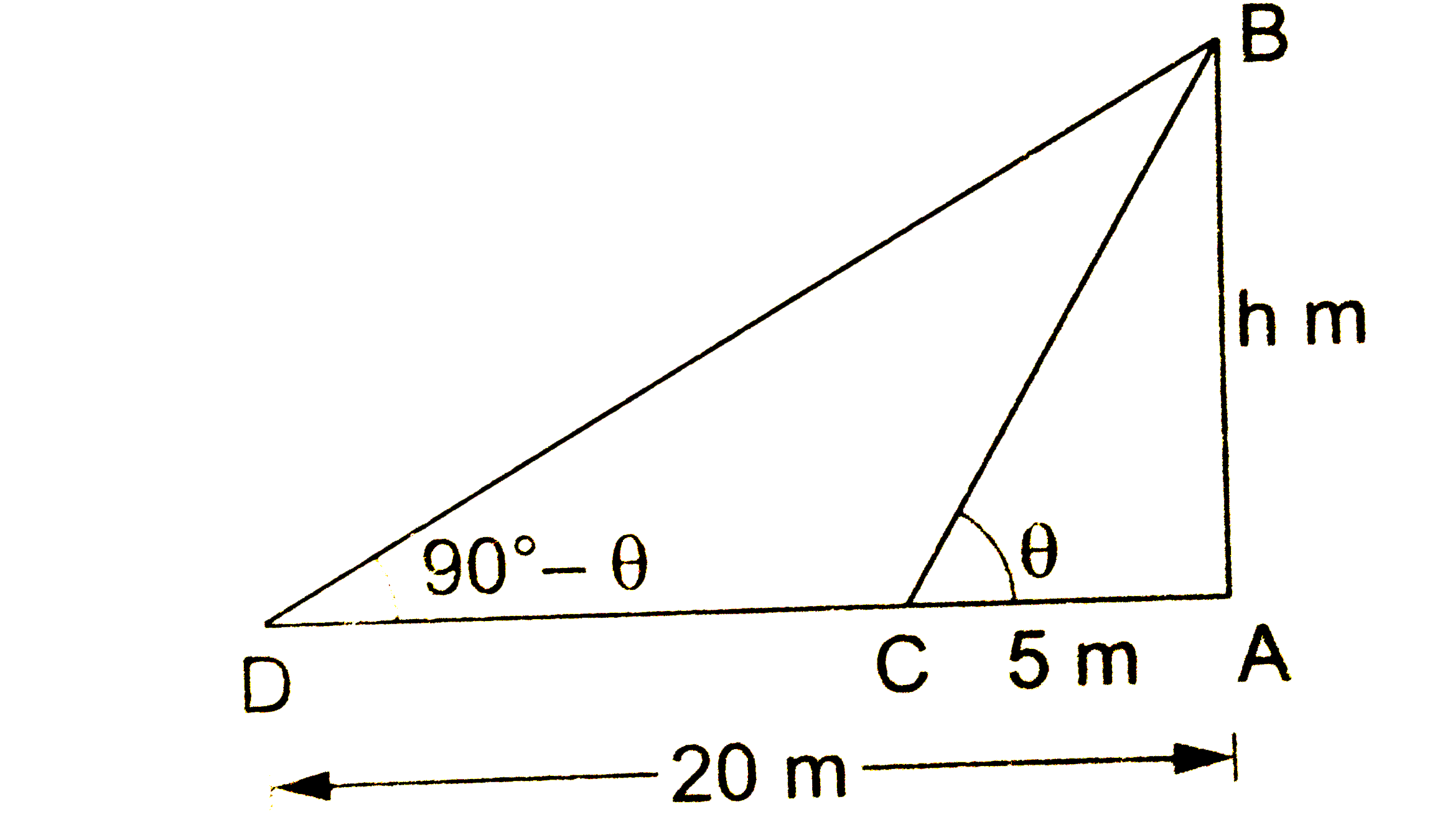
The anlge of the elevation of the top of a tower from two points at distances of 5 metre and 20 metres from the base of the tower and in the same straight line with it, are complementary. Find the height of the tower.
The correct Answer is:10m
ABAC=tanθ⇒h5=tanθ
⇒h=5tanθ……….(i).
ABAD=tan(90∘−θ)=cotθ
⇒=h20cotθ⇒h=20cotθ……..(ii)
Multiplying (i) and (ii), we get
∴h2=100tanθ×cotθ=100⇒h=10.
Topper's Solved these Questions
- HEIGHTS AND DISTANCESBOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Multiple Choice Questions (Mcq)
25 Videos
- HEIGHTS AND DISTANCESBOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Multiple Choice Questions (Mcq)
25 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
34 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - QUESTION
2 Videos
Similar Questions
If the angles of elevation of the top of a tower from two points at a distance of 4m and 9m from the base of the tower and in the same straight line with it are complementary, find the height of the tower.
View SolutionThe angles of elevation of the top of a tower from two points which are at distances of 10 m and 5 m from the base of the tower and in the same straight line with it are complementary. The height of the tower is :
View Solution
Knowledge Check
The angles of elevation of the top of a tower from two points which are at distances of 10 m and 5 m from the base of the tower and in the same straight line with it are complementary. The height of the tower is
A5mB15mC5√2mD75mThe angle of elevation of the top of a tower from the point P and Q at distance of a and b respectively from the base of the tower and in the same straight line with it are complementary .The height of the tower is
A√abBabCabDa2b2
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
View SolutionThe angle of elevation of the top of a tower from two points on the ground at distances a metres and b metres from the base of the tower and in the same straight line are complementary.Prove that height of the tower is√ab.
View SolutionThe angle of elevation of the top of a tower from two points at a distance of 4 m and 9 m from base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
OR
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower of the tower and in the same straight line with it are 60∘ and 30∘ respectively. Find the height of the tower.
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are 60∘and30∘ respectively . Find the height of the tower .
View SolutionThe angles of elevation of the top of a tower from two points at distances a and b metres from the base and in the same straight line with it are complementary. Prove that the height of the tower is √ab metres.
View Solution