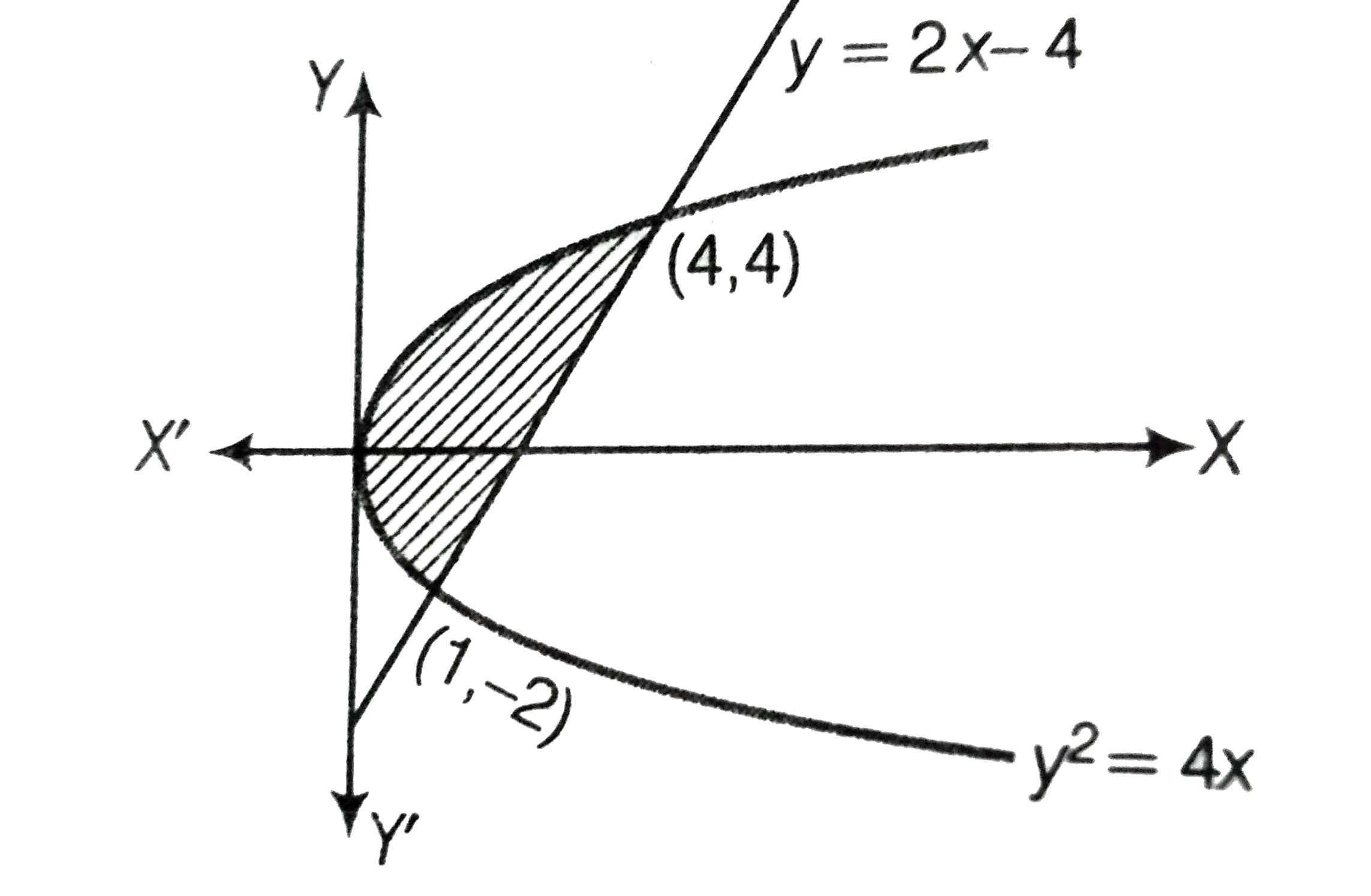
The area bounded between the parabola $y^{2} = 4 x$ and the line y = 2x - 4 is equal to

$\frac{17}{3}$ sq units

$\frac{19}{3}$ sq units

9 sq units

15 sq units

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

The area bounded by the parabola $y^{2} = 4 a x$ and the lines x = a and x = 4a, is
A $\frac{35 a^{2}}{3}$
B $\frac{4 a^{2}}{3}$
C $\frac{7 a^{2}}{3}$
D $\frac{56 a^{2}}{3}$
The area bounded by the parabola $x^{2} = 2 y$ and the line y=3x is
A4 sq. units
B18 sq. units
C24 sq. units
D32 sq. units
Area bounded between the curve $x^{2} = y$ and the line y = 4x is
A $\frac{32}{3}$ sq units
B $\frac{1}{3}$ sq unit
C $\frac{8}{3}$ sq units
D $\frac{16}{3}$ sq units