The area bounded by the curve f(x)=x+sinx and its inverse function between the ordinates x=0andx=2π is 4πsq.units (b) 8πsq.units 4sq.units (d) 8sq.unitsSolution in Bengali
y=x+sinx
∴ dydx=1+osx≥0∀x
Also d2ydx2=−sinx=0 when x=nπ,n∈Z
Hence x=nπ are points of inflection, where curve changes its concavity.
Also, for x∈(0,π),sinx>0⇒x+sinx>x
And for x∈(π,2π),sinx<0⇒x+sinx<x
Thus, we have following graphs of function y=f(x) and its inverse function.
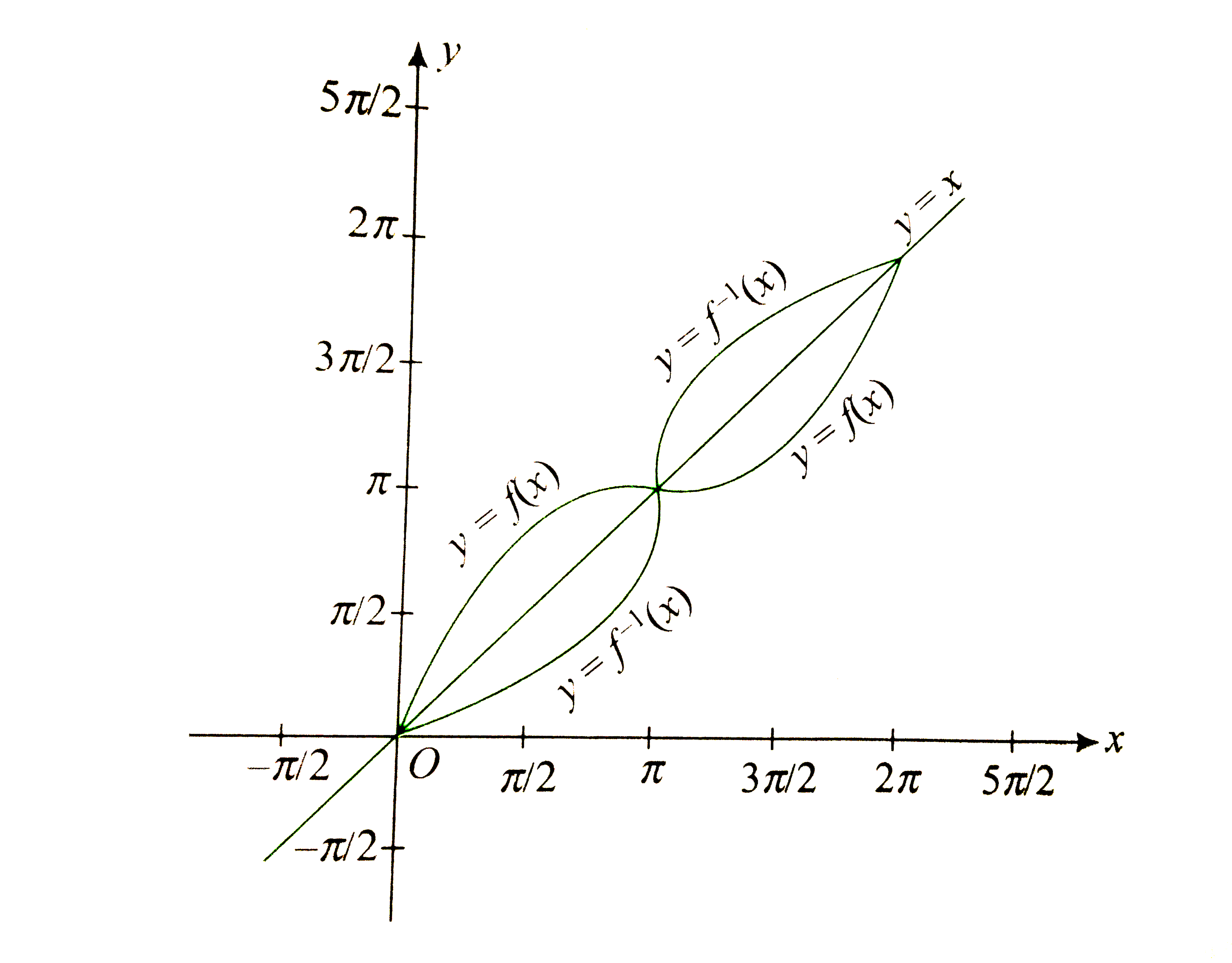
Required area =4∫π0(f(x)−x)dx
=4∫π0sinxdx=4×2=8 sq. units.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Solved Examples10videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.19videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
Similar Questions
Find the area bounded by the curve x2=y,x2=−yandy2=4x−3
11:48View SolutionFind the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
09:22View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
05:44View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is06:31View SolutionThe area enclosed between the curves y=(log)e(x+e),x=(log)e(1y), and the x-axis is 2sq.units (b) 1sq.units 4sq.units (d) none of these
08:39View SolutionThe area bounded by the curve f(x)=x+sinx and its inverse function between the ordinates x=0andx=2π is 4πsq.units (b) 8πsq.units 4sq.units (d) 8sq.units
12:16View SolutionLet f(x)=x3+3x+2andg(x) be the inverse of it. Then the area bounded by g(x) , the x-axis, and the ordinate at x=−2andx=6 is 14sq.units (b) 43sq.units 54sq.units (d) 73sq.units
06:28View SolutionIf f(x)=sinx,∀x∈[0,π2],f(x)+f(π−x)=2,∀x∈(π2,π)andf(x)=f(2π−x),∀x∈(π,2π), then the area enclosed by y=f(x) and the x-axis is πsq.units (b) 2πsq.units 2sq.units (d) 4sq.units
07:59View SolutionThe area of the closed figure bounded by x=−1,x=2,and y={−x2+2,x≤12x−1,x>1andtheabscissaaξsis 163sq.units (b) 103sq.units 133sq.units (d) 73sq.units
06:28View SolutionThe area enclosed between the curves y=(log)e(x+e),x=(log)e(1y), and the x-axis is (a) 2sq.units (b) 1sq.units (c) 4sq.units (d) none of these
06:10View SolutionA copper rod of mass m rests on two horizontal rails distance L apart and carries a current of I from one rail to the other. The coefficient of static friction between rod and rails is μs What are the (a) magnitude and (b) angle (relative to the vertical) of the smallest magnetic field that puts the rod on the verge of sliding?
03:35View SolutionLet f(x)=x3+3x+2andg(x) be the inverse of it. Then the area bounded by g(x) , the x-axis, and the ordinate at x=−2andx=6 is (a) 94sq.units (b) 43sq.units (c) 54sq.units (d) 73sq.units
05:57View SolutionThe area bounded by the loop of the curve 4y2=x2(4−x2) is (a)7/3 sq. units (b) 83sq.unites 113sq.units (d) 163sq.units
01:13View SolutionA particle of mass m is moving anticlockwise, in a circle of radius R in x−y plane with centre at (R,0) with a constant speed v2. If is located at point (2R,0) at time t=0. A man starts moving with a velocity v1 along the positive y-axis from origin at t=0. Calculate the linear momentum of the particle w.r.t. man as a function of time.
05:06View SolutionThe area of the closed figure bounded by y=x22−2x+2 and the tangents to it at (1,12)and(4,2) is 98sq.units (b) 38sq.units 32sq.units (d) 94sq.units
07:49View SolutionThe area bounded by the y=2−x2and x+y=0 is (a)72sq.units b. 92 sq.units c. 9 sq.units d. none of these
11:07View Solution

