The area bounded by the curves $y = \sqrt{x}, 2 y - x + 3 = 0,$ X-axis and lying in the first quadrant is

A

9

B

36

C

18

D

$27 / 4$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Required area A is given by
$A = 3 \int 0 (x_{2} - x_{1}) d y$

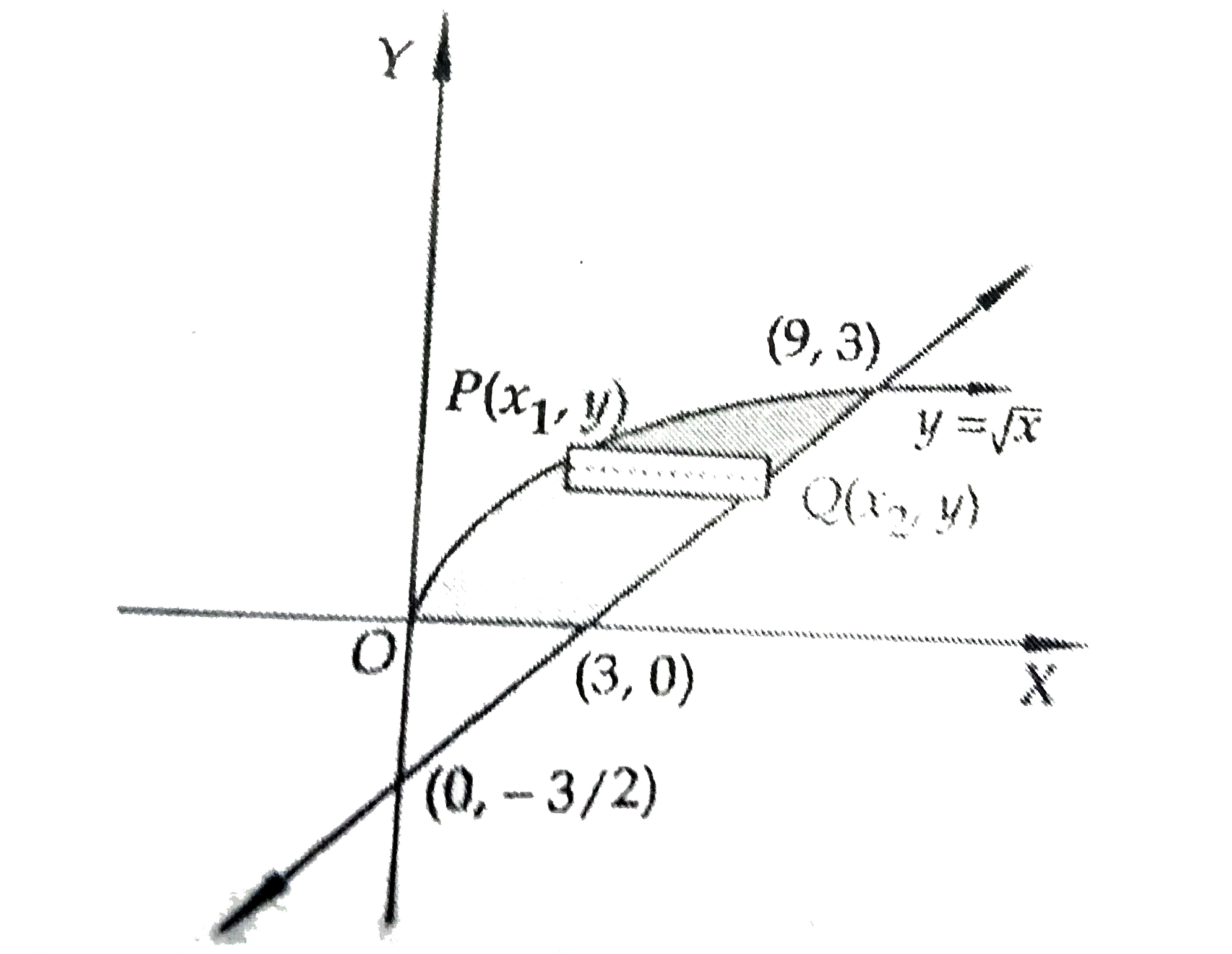
$\Rightarrow A = 3 2 y + 3 - y^{2} 0 d y {[y^{2} + 3 y - \frac{y^{3}}{3}]}_{0}^{2} = 9 + 9 - 9 = 9$

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMACHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Exercise
62 Videos
AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMACHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Chapter Test
60 Videos
APPLICATION OF DERIVATIVESBOOK - OBJECTIVE RD SHARMACHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Illustration
6 Videos
CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31 Videos

Similar Questions

Knowledge Check

The area (in square units) bounded by the curves $y = \sqrt{x}, 2 y - x + 3 = 0,$ x-axis, and lying in the first quadrant is
A9
B36
C18
D $\frac{27}{4}$
The area (in square units) bounded by the curves $y = \sqrt{x}, 2 y - x + 3 = 0,$ x-axis, and lying in the first quadrant is
A9
B36
C18
D $\frac{27}{4}$
The area bounded by the curve $y = sin 2 x,$ axis and $y = 1,$ is
A1
B $1 / 4$
C $π / 4$
D $π / 4 - 1 / 2$

OBJECTIVE RD SHARMA-AREAS OF BOUNDED REGIONS-Chapter Test

Home
Ask Doubt
Profile