The area bounded by the curves y=√x,2y−x+3=0, X-axis and lying in the first quadrant is
9
36
18
274
y=√xand2y−x+3=0
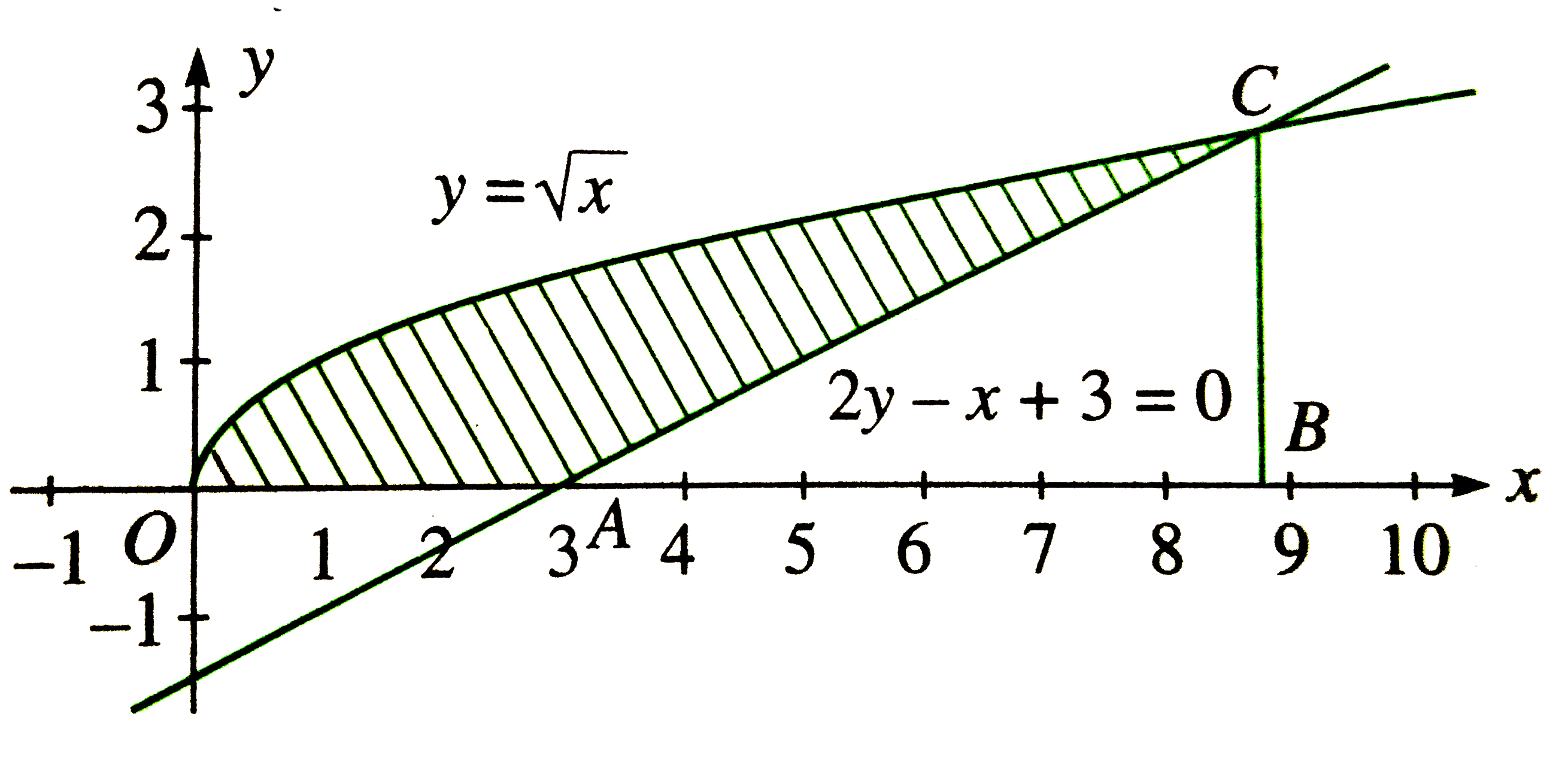
∴ Required area = Area of region OABCO-Area of ΔABC
=9∫0√xdx−12×BC×AB
=(x3/23/2)90−12×3×6
=9 sq. units
Similar Questions
Area bounded by the curves : y=√x,x=2y+3 in the first quadrant and x-axis is :
View SolutionThe area (in square units) bounded by the curves : y=sqrtx, 2y-x +3 =0 x-axis , and lying in the first quadrant is :
View SolutionThe area bounded by the curves y=√x,2y−x+3=0, x-axis and lying in the first quadrant is
View SolutionFind the area bounded by the curve y=√x,x=2y+3 in the first quadrant and X-axis.
View SolutionThe area (in square units) bounded by the curves y=sqrt(x),2y-x+3=0, x-axis, and lying in the first quadrant is
View SolutionFind the area of the region bounded by y=√x, x=2y+3 in the first quadrant and x-axis.
View Solutionवक्रो y=√x,2y−x+3=0 तथा x-अक्ष से घिरे उस क्षेत्र, जो प्रथम चतुर्थांश में स्थित है, का (वर्ग इकाई में) क्षेत्रफल है -
View SolutionArea bounded by the curves : y=√x,x=2y+3 in the first quadrant and x-axis is :
View Solution
