The area enclosed between the curve $y = \log_{e} (x + e)$ and the coordinate axes is

A

4

B

3

C

2

D

1

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

The area enclosed by $y = \log_{e} (x + e)$ and the coorcinate axes is shaded in Fig. 17.

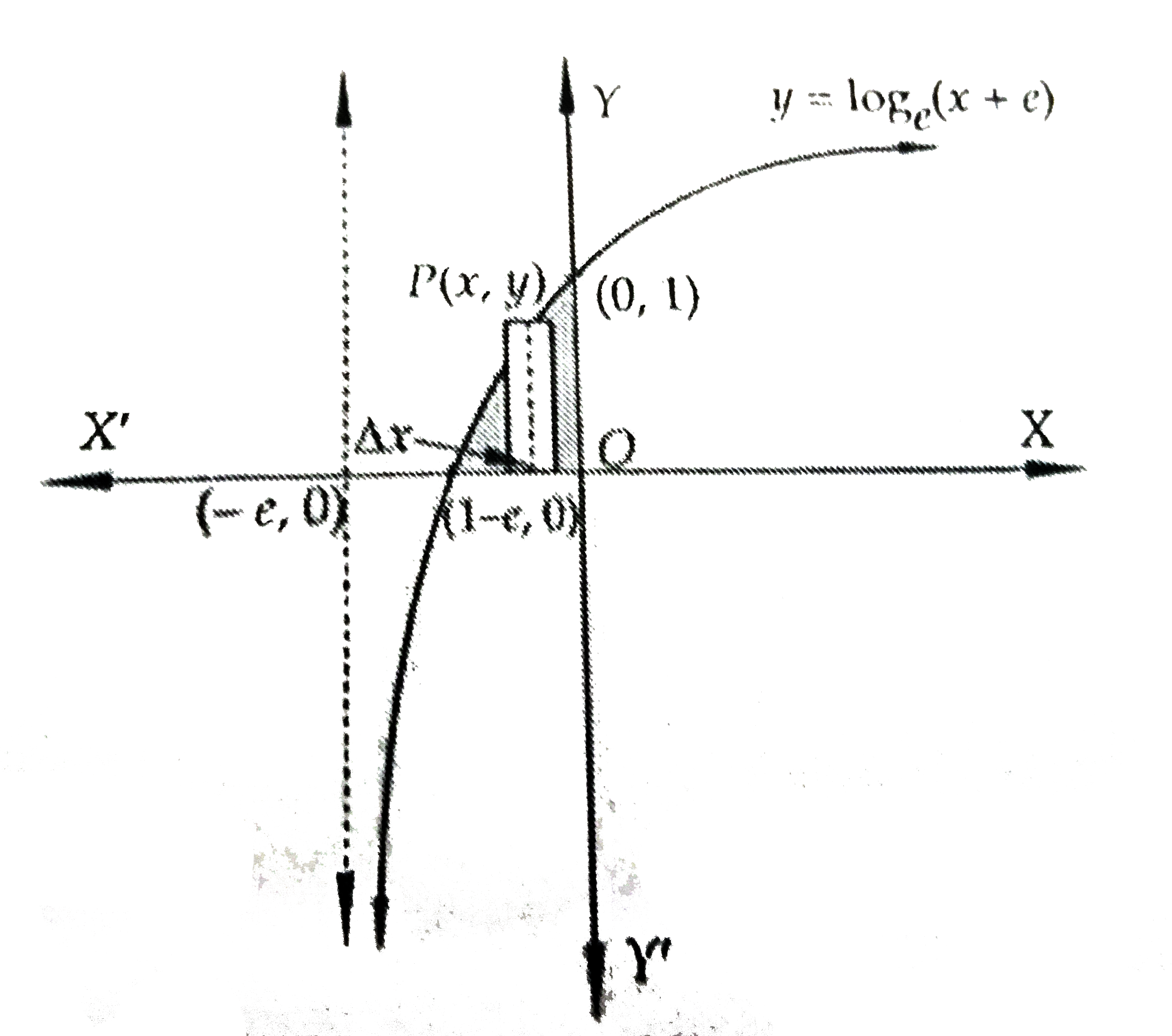
Let A be the required area. Then,
$A = \underset{1 - e}{\int^{0}} y d x = \underset{1 - e}{\int^{0}} \log_{e} (x + e) d x$
$\Rightarrow A = {[x \log_{e} (x + e)]}_{1 - e}^{0} - \underset{1 - e}{\int^{0}} \frac{x}{x + e} d x$
$\Rightarrow A = {[x \log_{e} (x + e)]}_{1 - e}^{0} - {[x - e \log_{e} (x + e)]}_{1 - e}^{0}$
$\Rightarrow A = 0 - [(0 - e) - (1 - e) + 0] = 1$ sq. units

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area enclosed between the curve $y = {log}_{e} (x + e)$ and the coordinate axes is
A3
B4
C1
D2
Question 2 - Select One
The area enclosed between the curves $y = x^{3}$ and $y = \sqrt{x}$ is
A $\frac{5}{3}$ sq units
B $\frac{5}{4}$ sq units
C $\frac{5}{12}$ sq unit
D $\frac{12}{5}$ sq units
Question 3 - Select One
Area enclosed between the curve $y = x^{2}$ and the line y = x is
A $\frac{1}{8}$
B $\frac{1}{6}$
C $\frac{3}{2}$
D $\frac{1}{7}$

OBJECTIVE RD SHARMA-AREAS OF BOUNDED REGIONS-Chapter Test

Home
Ask Doubt
Profile