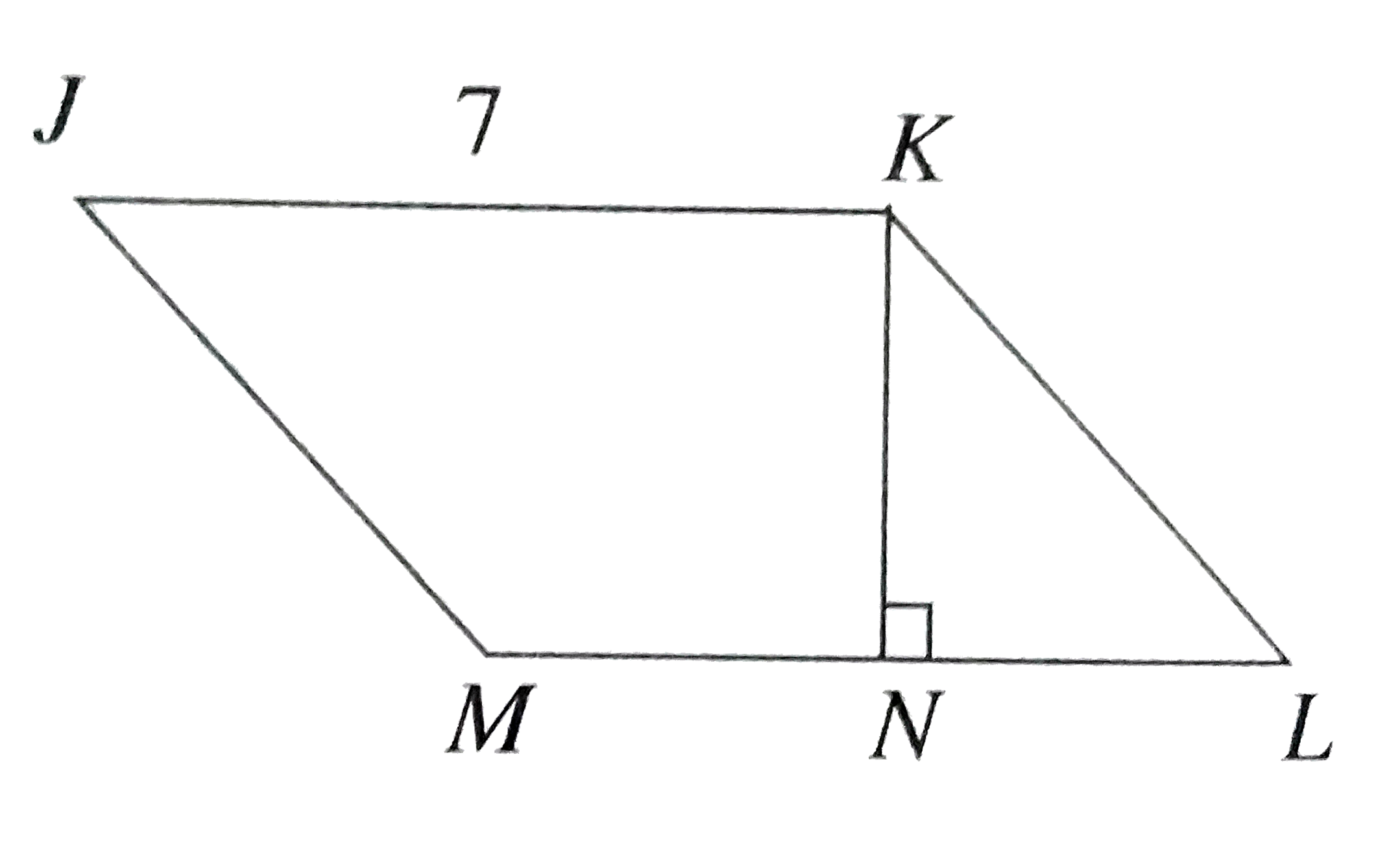
The area of parallelogram JKLM is 28 ¯¯¯¯¯¯JK=7. If ¯¯¯¯¯¯¯KN is perpendicular to ¯¯¯¯¯¯¯ML and if N is the midpoint of ¯¯¯¯¯¯¯ML, what is the perimeter of JKLM ?
24.6302
23.25
28
31.596
The correct Answer is:A
Because JKLM is a parallelogram, opposite sides are equal and ¯¯¯¯¯¯¯ML=7. Midpoint N divides that 7 into two equal pices of 72 each. The area of the parallelogram, which is equal to the base times the height, is given as 28, and because the base is 7, altitude ¯¯¯¯¯¯¯KN=4. Put all this into the figure.
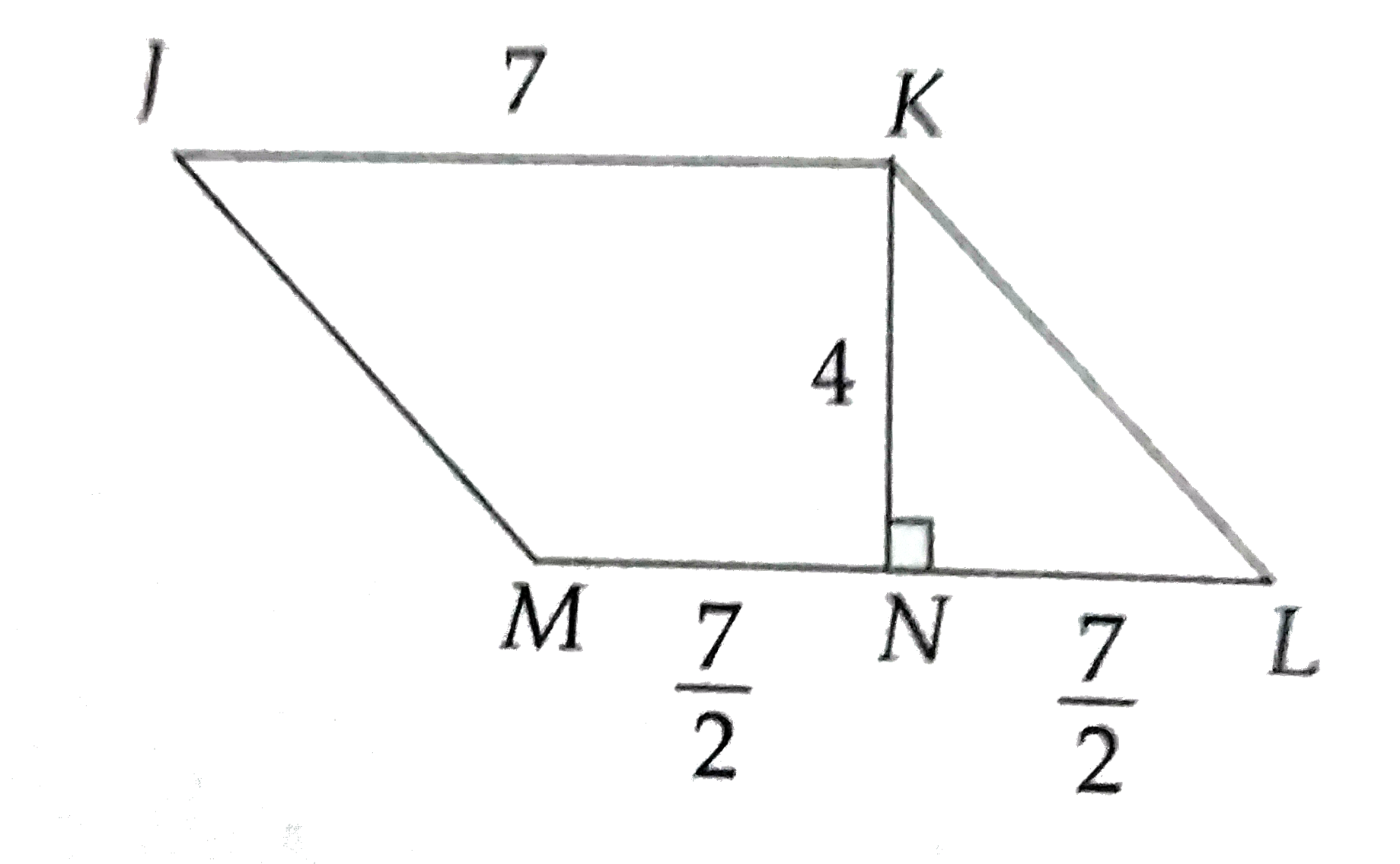
Use the Pythagorean theorem to determine the length of ¯¯¯¯¯¯KL.
¯¯¯¯¯¯LN2+¯¯¯¯¯¯¯KN2=¯¯¯¯¯¯KL2
(72)2+42=¯¯¯¯¯¯KL2
494+16=¯¯¯¯¯¯KL2
494+644=¯¯¯¯¯¯KL2
1134=¯¯¯¯¯¯KL2
√1134=¯¯¯¯¯¯KL≈5.3151
Now add all the sides of the parallelogram to find the perimeter : 7+7+5.3151=24.6302.
Topper's Solved these Questions
- PLANE GEOMETRY BOOK - KAPLANCHAPTER - PLANE GEOMETRY EXERCISE - PLANE GEOMETRY FOLLOW - UP TEST
6 Videos
- MISCELLANEOUS TOPICS BOOK - KAPLANCHAPTER - MISCELLANEOUS TOPICS EXERCISE - MISCELLANEOUS TOPICS FOLLOW - UP TEST
12 Videos
- PRACTICE TEST 1 BOOK - KAPLANCHAPTER - PRACTICE TEST 1 EXERCISE - PRACTICE TEST
50 Videos
Similar Questions
Knowledge Check
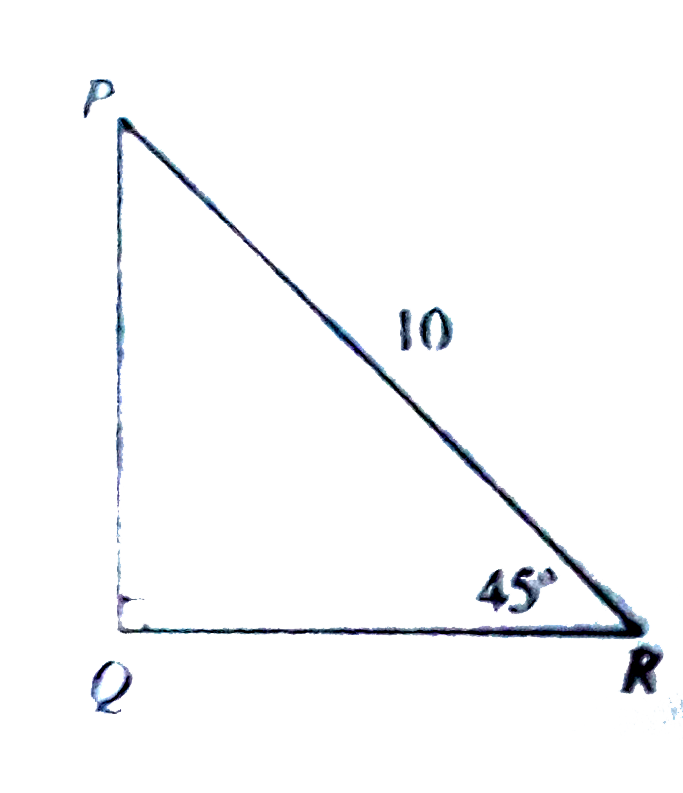
What is the length of ¯¯¯¯¯¯QR ?A5B5√22C10√2D5√2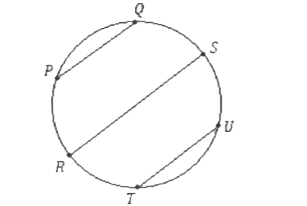
In the circle above with diameter d, chords ¯¯¯¯¯¯PQand¯¯¯¯¯¯TU are parallel to diameter ¯¯¯¯¯RS. If ¯¯¯¯¯¯PQand¯¯¯¯¯¯TU are each 34 of the length of ¯¯¯¯¯RS, what is the distance between chords ¯¯¯¯¯¯PQand¯¯¯¯¯¯TU in terms of d?Ad√78Bd√74Cπd4D3πd4In △ACD below, B is on ¯¯¯¯¯¯AC, E is on ¯¯¯¯¯¯AD, the measure of ∠CAD is 28∘, and ¯¯¯¯¯¯AD is perpendicular to both ¯¯¯¯¯¯BE and ¯¯¯¯¯¯CD. What is the measure of ∠CBE?
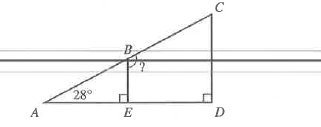 A104∘B118∘C124∘D146∘
A104∘B118∘C124∘D146∘
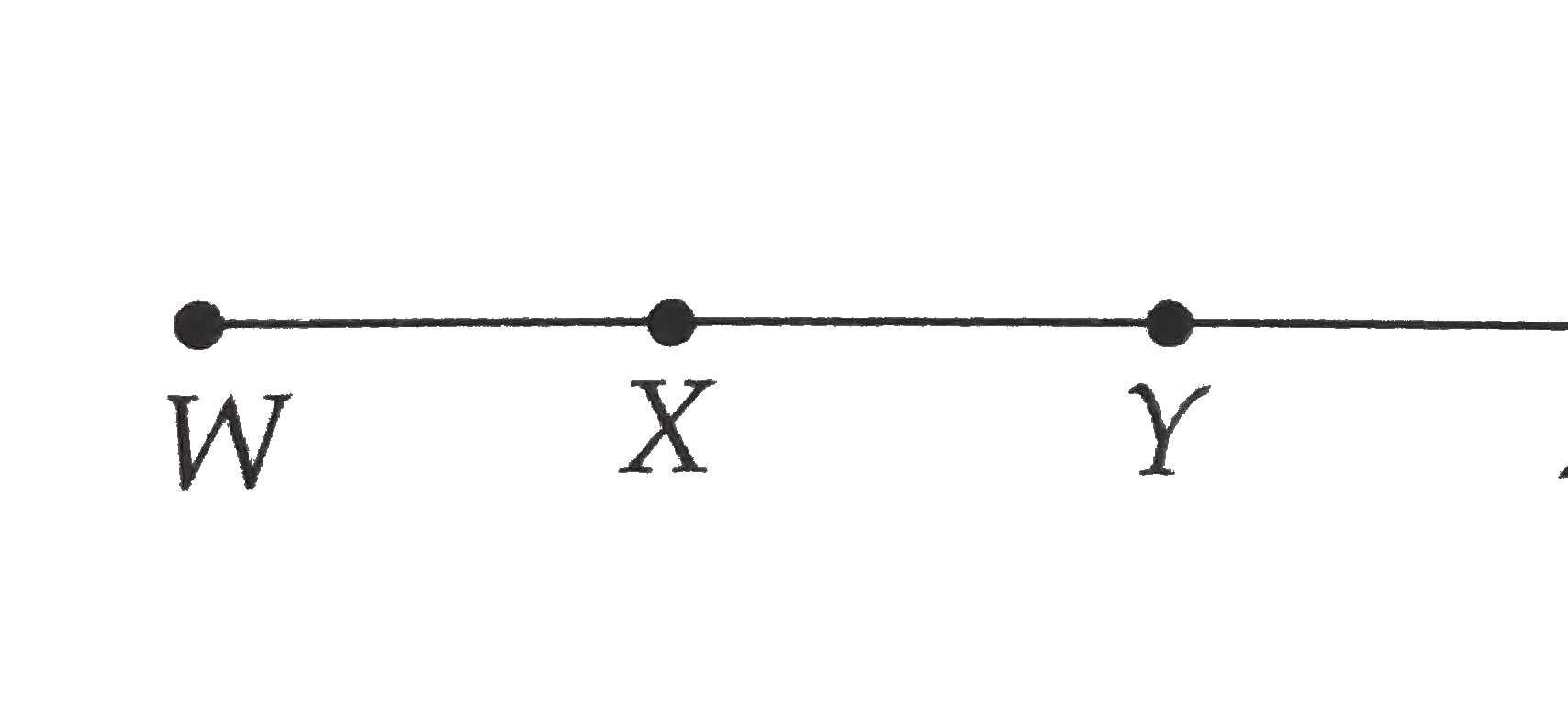
The length of ¯¯¯¯¯¯¯WZ is 3a+15, and the length of ¯¯¯¯¯¯¯WX is 7a+5. If Y is the midpoint of ¯¯¯¯¯¯XZ, what is the length of ¯¯¯¯¯¯¯WY ?
View Solution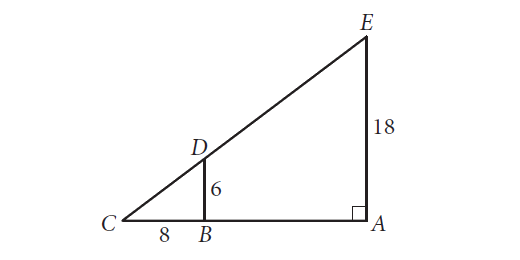
In the figure above, ¯¯¯¯¯¯BD is parallel to ¯¯¯¯¯¯AE. What is the length of ¯¯¯¯¯¯CE ?
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
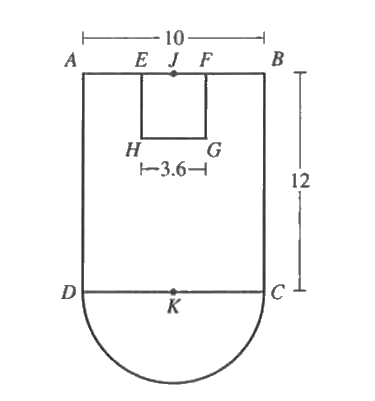
What is the length, in meters, of are ¯¯¯¯¯¯CD?
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
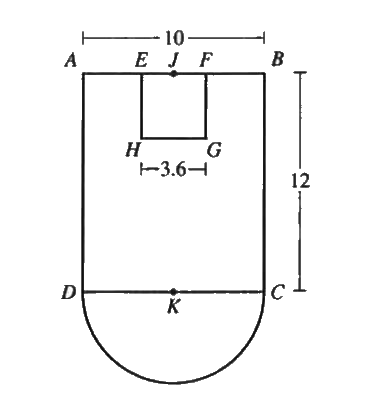
What is the length, in meters, of ¯¯¯¯¯¯JD?
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
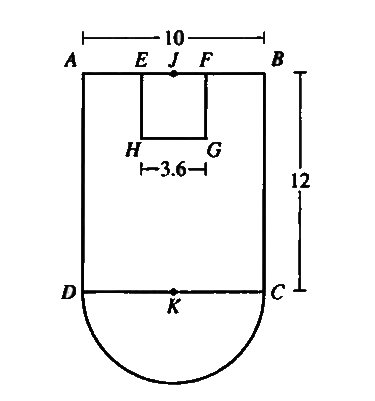
The length of ¯¯¯¯¯¯EH is what precent of the length of ¯¯¯¯¯¯AD?
View Solution