What is the distance from the midpoint of ¯¯¯¯¯¯EF to the midpoint of ¯¯¯¯¯¯¯GH ?

5.408
5.454
5.568
5.59
The correct Answer is:D
To find the midpoint of a segment, average the x - coordinates and average the y - coordinates of the endpoints :
midpoint of ¯¯¯¯¯¯EF=(−3+(−2)2,3+(−4)2)=(−52,−12)
midpoint of ¯¯¯¯¯¯¯GH=(1+52,3+(−2)2)=(3,12)
To find the distance between two points, use the distance formula :
Distance =√(x2−x1)2+(y2−y1)2
=√(3−(−52))2+(12−(−12))2
=√(112)2+(1)2
=√30.25+1
=√31.25≈5.590
Topper's Solved these Questions
- COORDINATE GEOMETRY BOOK - KAPLANCHAPTER - COORDINATE GEOMETRY EXERCISE - COORDINATE GEOMETRY FOLLOW - UP TEST
6 Videos
- CIRCLESBOOK - KAPLANCHAPTER - CIRCLESEXERCISE - Multiple Choice Question
12 Videos
- EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONS BOOK - KAPLANCHAPTER - EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONS EXERCISE - Multiple Choice Question
20 Videos
Similar Questions
A, B, C, and D all lie on a number line. C is the midpoint of ¯¯¯¯¯¯AB and D is the midpoint of ¯¯¯¯¯¯AC.
Quantity AQuantity BThe ratio of ¯¯¯¯¯¯AD to ¯¯¯¯¯¯CBThe ratio of ¯¯¯¯¯¯AC to ¯¯¯¯¯¯AB
View SolutionThe ratio of ¯¯¯¯¯¯DB to ¯¯¯¯¯¯EF is 4 to 9. If ¯¯¯¯¯¯DF=2, what is the distance from D to the midpont of ¯¯¯¯¯¯EF ?
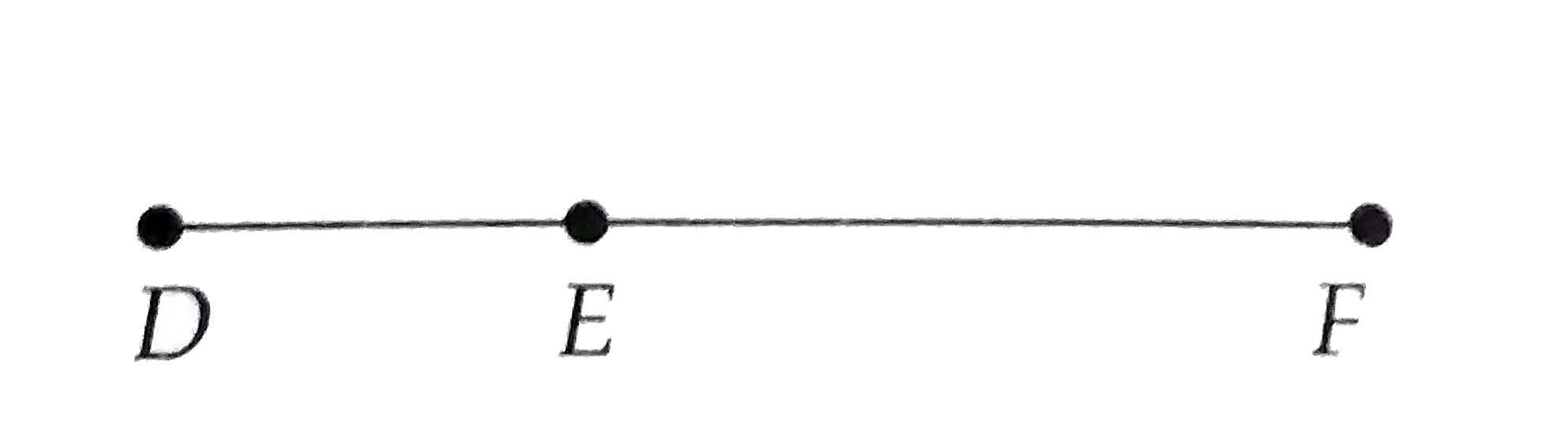
View Solution
Knowledge Check
The points P,Q,R and S lie in that order on a straight line . The midpoint of ¯¯¯¯¯¯QS is R and the midpoint of ¯¯¯¯¯PS is Q . The length of ¯¯¯¯¯¯QR is x feet and the length of ¯¯¯¯¯¯PQ is 4x−16 feet . What is the length , in feet , of ¯¯¯¯¯PS?
A32B20C16D8In the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
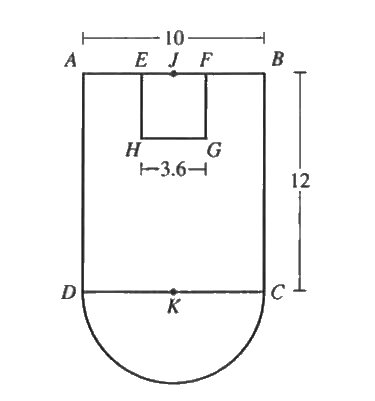
The figure will be placed in the standard (x,y) coordinate plane so that K is at the origin , ¯¯¯¯¯¯AB is parallel to the x-axis, and 1 meter equal 1 coordinates unit. Which of the following values could be the y-coordinate of H?A1.8B3.6C8.4D10In the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
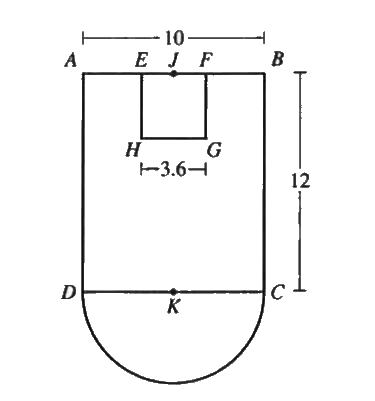
What is the length, in meters, of ¯¯¯¯¯¯JD?A13B15.6C17D√44
In triangle ABC,D is the midpoint of AB, E is the midpoint of DB and F is the midpoint of BC. If the area of ΔABC is 96, the area of ΔAEF is
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
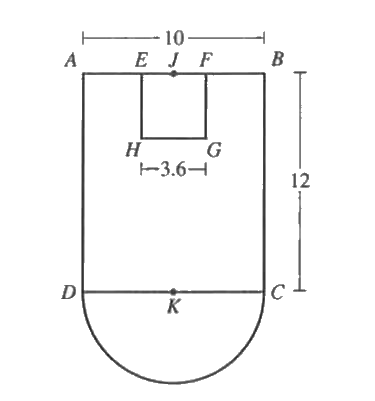
What is the length, in meters, of are ¯¯¯¯¯¯CD?
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
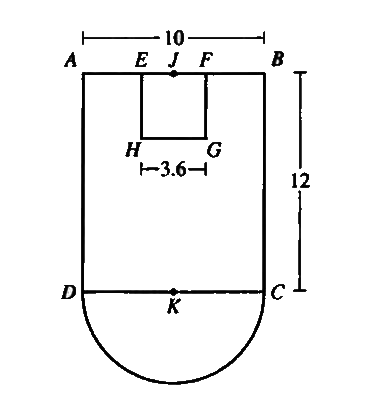
The length of ¯¯¯¯¯¯EH is what precent of the length of ¯¯¯¯¯¯AD?
View Solution
What is the length of ¯¯¯¯¯¯QR ?
View SolutionPoint A, B, and C all lie on a line. Point D is midpoint of ¯¯¯¯¯¯AB and E is the midpoint of BC,¯¯¯¯¯¯AB=4and¯¯¯¯¯¯BC=10. Which of the following could be the length of ¯¯¯¯¯¯AE?
View Solution
