The area of the region bounded by the curve C:y=x+1x2+1 nad the line y=1 , is
ml −12In2+π4
In2−π4+1
12In2+π4−1
In 2−π2+1
The correct Answer is:c
Let A be the required area. Then,
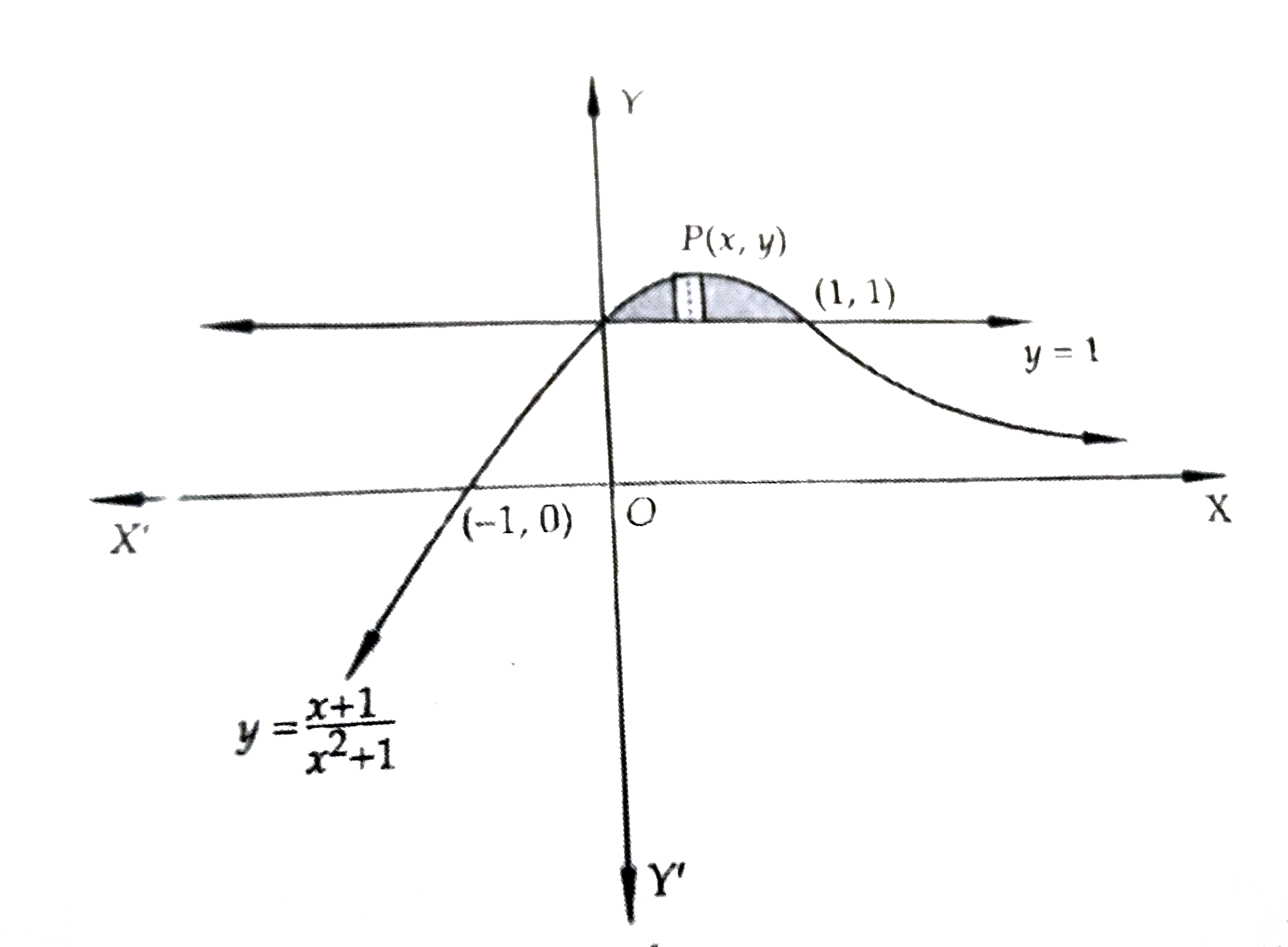
A=1y−10dx=1x+1x2+1−10dx
⇒A=112log(x2+1)+tan2x−x010=12In 2+π4−1
Topper's Solved these Questions
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Exercise
61 Videos
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Chapter Test
60 Videos
- ALGEBRAIC INEQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRAIC INEQUATIONSEXERCISE - Exercise
39 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
30 Videos
Similar Questions
The area of the region bounded by the curve y=x3 , and the lines , y=8 and x=0, is
View SolutionThe area of the region bounded by the curve y = x + 1 and the lines x=2,x=3, is
View SolutionThe area of the region bounded by the circle x2+y2=1 and the line x+y=1 is :
View SolutionThe area of the region bounded by the curve y=x2−2 and line y = 2 , is equal to
View SolutionThe area of the region bounded by the curves y=xex,y=ex and the lines x=±1, is equal to
View SolutionThe area of the region bounded by the curves y=x2andy=21+x2 is
View SolutionThe area of the region bounded by the curve y=|x−1| and y=1 is:
View SolutionA body weighs w Newton on the surface of the earth. Its weight at a height equal to half the radius of the earth, will be xyw where x and y are coprimes . Find x and y
View SolutionFind the area of the region bounded by the curve y=x2−2x, the x-axis and the lines x=1andx=−1
View SolutionThe area of the region bounded by the curve y=x2 and y = x is equal to
View Solution
