The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m. Find t
To solve the problem, we need to find the length of the segment PQ on the suspension bridge cable, which hangs in the form of a parabola. Here are the steps to find the solution:
Step 1: Understand the Geometry
We have a suspension bridge with a horizontal roadway of length 100 m. The longest vertical wire from the cable to the roadway is 30 m, and the shortest is 6 m. The distance between the points where the wires are attached to the cable is 100 m.
Step 2: Define the Points
Let:
- Point A be the point where the longest wire (30 m) is attached.
- Point B be the point where the shortest wire (6 m) is attached.
- The horizontal distance between points A and B is 100 m.
Step 3: Determine the Coordinates
Assume:
- Point A is at (0,30) (the origin is at the lowest point of the cable).
- Point B is at (100,6).
Step 4: Find the Equation of the Parabola
The general equation of a parabola that opens downwards is given by:
y=ax2+bx+c
Since the vertex is at the lowest point, we can simplify this to:
y=−14ax2+h
where h is the height at the vertex, and a is a constant.
Step 5: Use the Points to Form Equations
Using the coordinates of points A and B:
1. For point A(0,30):
30=−14a(02)+h⟹h=30
2. For point B(100,6):
6=−14a(1002)+30
Simplifying this gives:
6=−100004a+30⟹−100004a=6−30⟹−100004a=−24
100004a=24⟹4a=1000024⟹a=250024
Step 6: Find the Length of Segment PQ
Let PQ be the segment at a distance of 18 m from the lowest point of the cable. The height at this point is:
h−18=30−18=12
Now, we need to find the x-coordinates where y=12:
12=−14ax2+30
Substituting a:
12=−242500x2+30
Rearranging gives:
−242500x2=12−30⟹−242500x2=−18
242500x2=18⟹x2=18×250024=1875
Taking the square root:
x=√1875≈43.3 m
Step 7: Calculate Length PQ
The length of segment PQ is the difference in heights of the wires at this point:
PQ=30−12=18 m
Final Answer
The length of segment PQ is approximately 18 m.
We have a suspension bridge with a horizontal roadway of length 100 m. The longest vertical wire from the cable to the roadway is 30 m, and the shortest is 6 m. The distance between the points where the wires are attached to the cable is 100 m.
Let:
- Point A be the point where the longest wire (30 m) is attached.
- Point B be the point where the shortest wire (6 m) is attached.
- The horizontal distance between points A and B is 100 m.
Assume:
- Point A is at (0,30) (the origin is at the lowest point of the cable).
- Point B is at (100,6).
The general equation of a parabola that opens downwards is given by:
y=ax2+bx+c
Since the vertex is at the lowest point, we can simplify this to:
y=−14ax2+h
where h is the height at the vertex, and a is a constant.
Using the coordinates of points A and B:
1. For point A(0,30):
30=−14a(02)+h⟹h=30
2. For point B(100,6):
6=−14a(1002)+30
Simplifying this gives:
6=−100004a+30⟹−100004a=6−30⟹−100004a=−24
100004a=24⟹4a=1000024⟹a=250024
Let PQ be the segment at a distance of 18 m from the lowest point of the cable. The height at this point is:
h−18=30−18=12
Now, we need to find the x-coordinates where y=12:
12=−14ax2+30
Substituting a:
12=−242500x2+30
Rearranging gives:
−242500x2=12−30⟹−242500x2=−18
242500x2=18⟹x2=18×250024=1875
Taking the square root:
x=√1875≈43.3 m
The length of segment PQ is the difference in heights of the wires at this point:
PQ=30−12=18 m
The length of segment PQ is approximately 18 m.
Topper's Solved these Questions
- CONIC SECTIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONIC SECTIONEXERCISE - Exercise 11.4
15 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATION BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATION EXERCISE - MISCELLANEOUS EXERCISE
20 Videos
- INTRODUCTION OF THREE DIMENSIONAL GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION OF THREE DIMENSIONAL GEOMETRYEXERCISE - Miscellaneous Exercise
6 Videos
Similar Questions
The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100m long is supported by vertical wires attached to the cable, the longest wire being 30m and the shortest being 6m. Find the length of the supporting wire attached to the roadway 18m from the middle.
View SolutionIf the distribution of weight is uniform, then the rope of the suspended bridge takes the form of parabola.The height of the supporting towers is 20m, the distance between these towers is 150m and the height of the lowest point of the rope from the road is 3m. Find the equation of the parabolic shape of the rope considering the floor of the parabolic shape of the rope considering the floor of the bridge as X-axis and the axis of the parabola as Y-axis. Find the height of that tower which supports the rope and is at a distance of 30 m from the centre of the road.
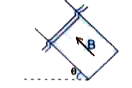
View SolutionA wire of length l, mass m and resistance R slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle θ with the horizontal and a uniform vertical magnetic field of the inducetion B exists throughout the rregion. Find the steady state velocity of the wire.
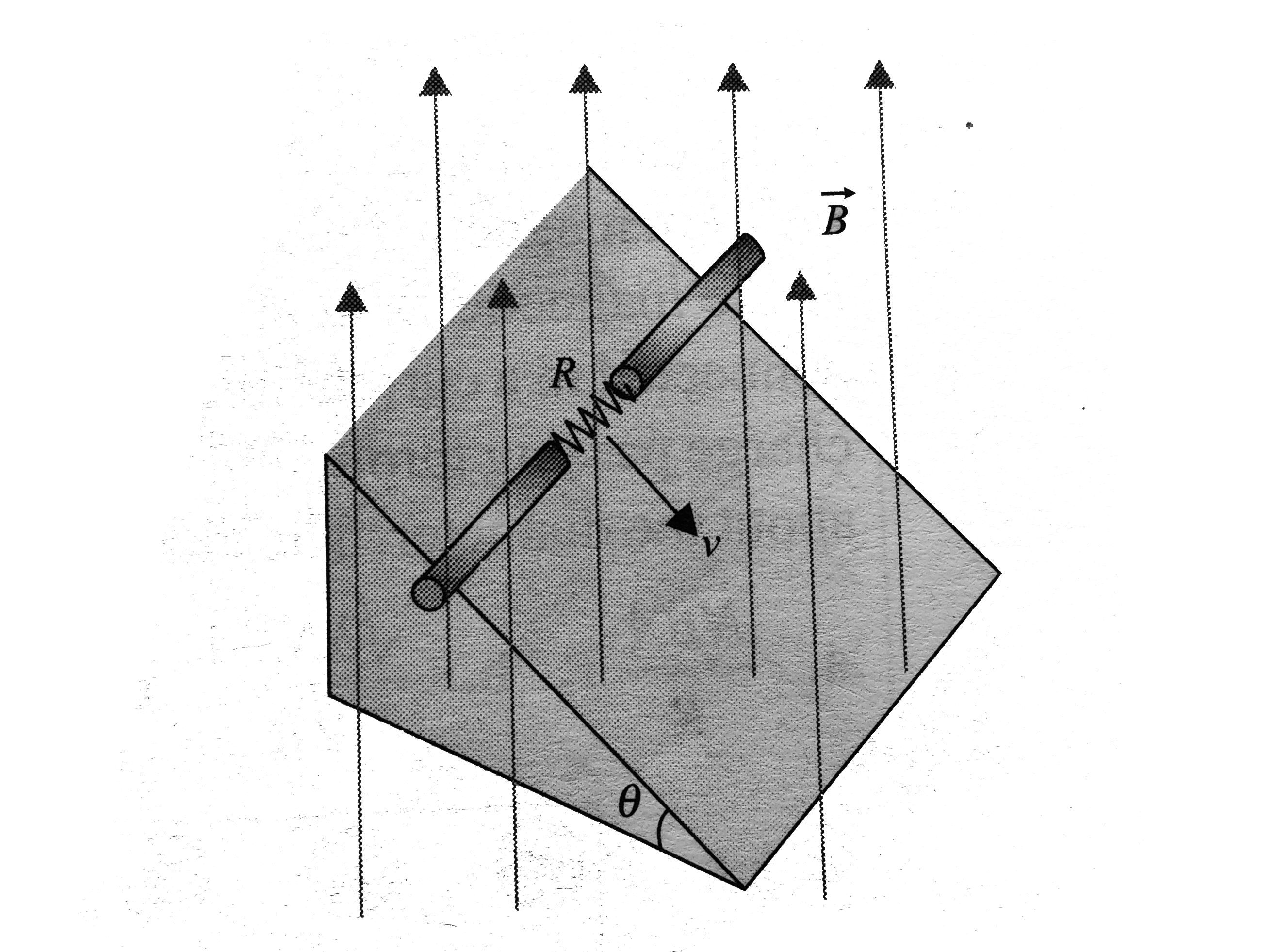
View SolutionA wire of length l, mass m and resitance R slides without any friction down the parallel conducting rails of negligible resistance (Fig). The rails are connected to the wire so that the wire and the rails form a closed rectangular conducting loop. The plane of the rails makes an angle θ with the horizontal and a uniform vertical magnetic field of induction B exists throughout the region. Find the steady-state velocity of the wire
View SolutionA brilliant student of physics developed a magnetic balance to weight objects. The mass m to be measured is hung from the center the bar. Bar is kept in a uniform magnetic field of 1.5T directed into the plane of the figure. Battery voltage can be adjusted to vary the current in the circuit. The horizontal bar shown is 60cm long and is made of extremly light weight material. It is connected to the battery via a resistance. There is no tension in the supporting wired. The magnetic force only supports the hanging weight.
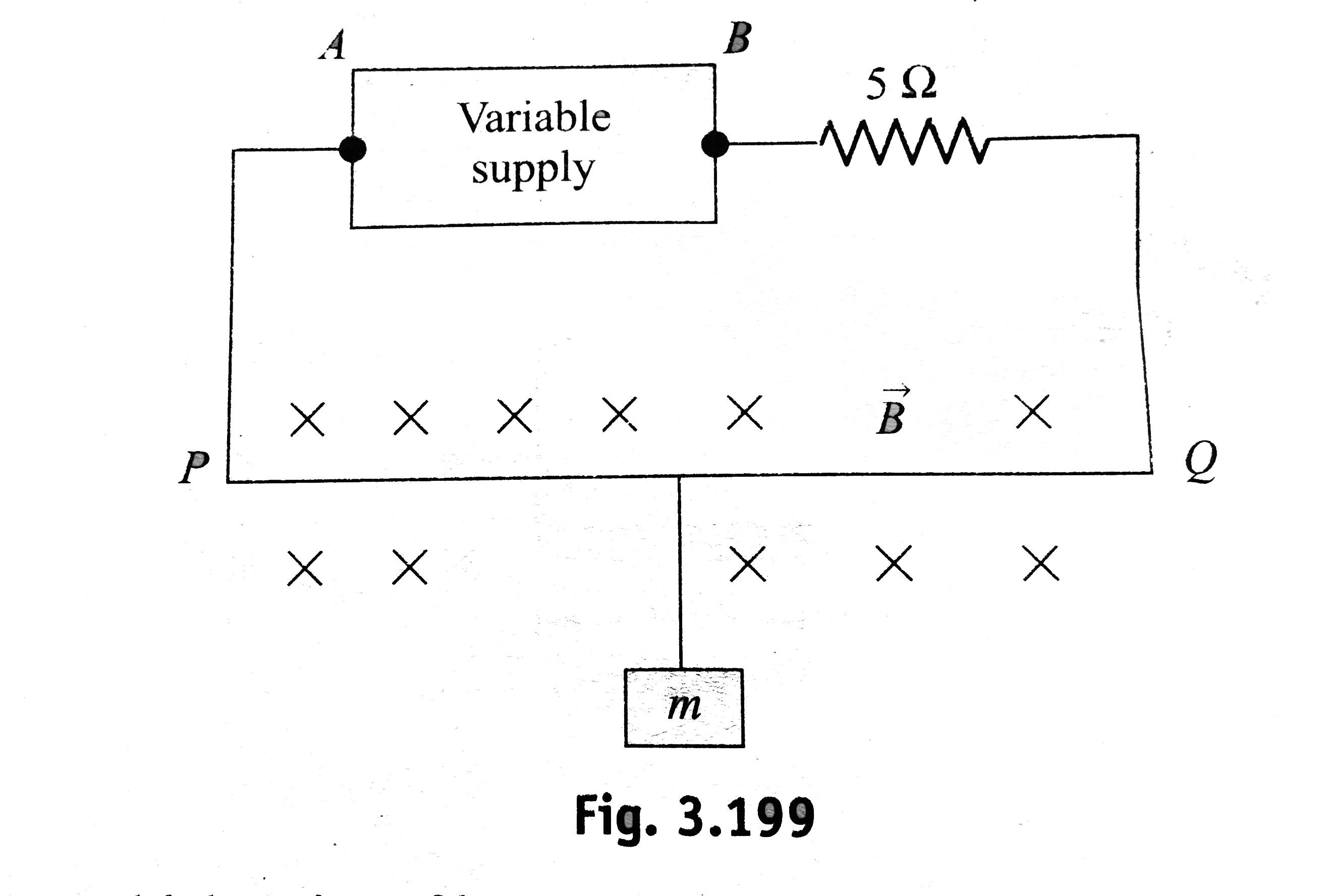
If V=150V, what is the maximum mass m ?
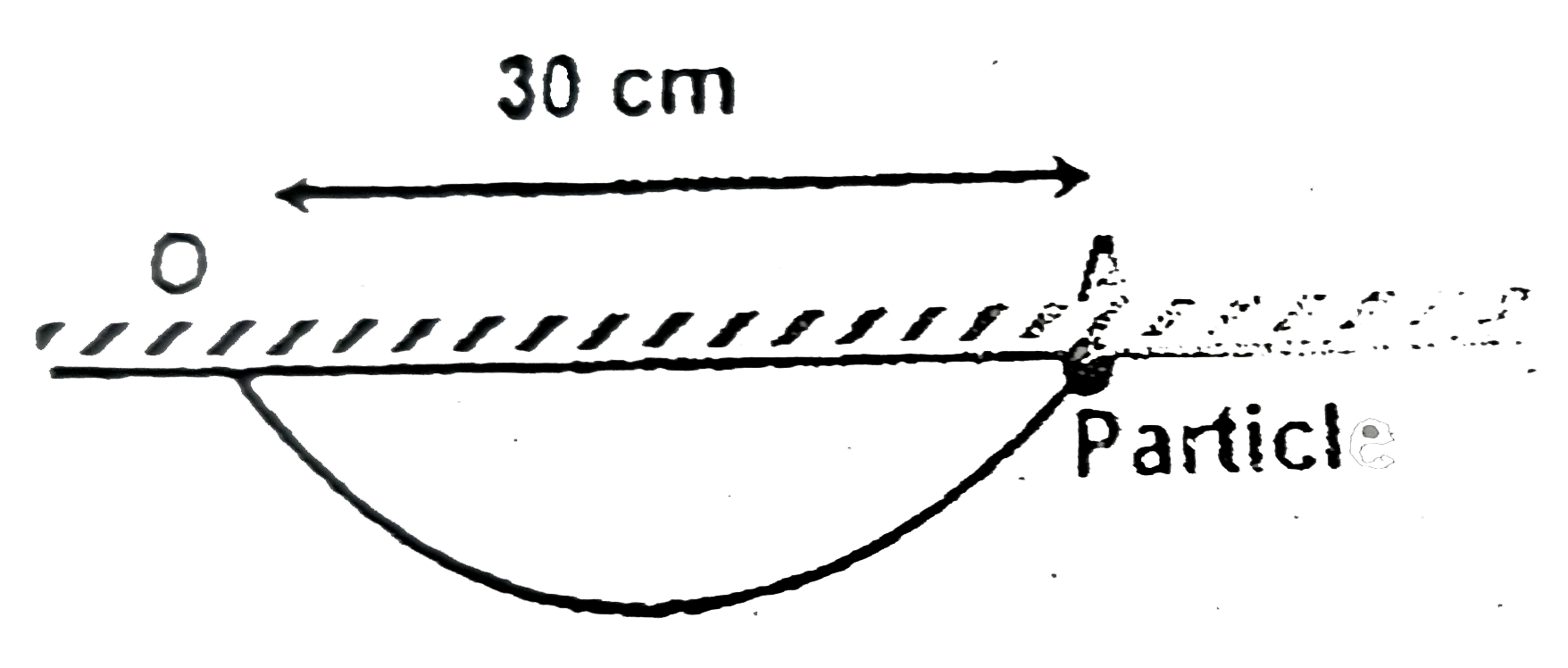
View SolutionA small ball of mass 100g is attached to a light and inextensible string of length 50cm. The string is tied to a support O and the mass m released from point A which is a' a horizontal distance of 30cm from the support. Calculate the speed of the ball is its lowest point of the trajectory.
View SolutionA brilliant student of physics developed a magnetic balance to weight objects. The mass m to be measured is hung from the center the bar. Bar is kept in a uniform magnetic field of 1.5T directed into the plane of the figure. Battery voltage can be adjusted to vary the current in the circuit. The horizontal bar shown is 60cm long and is made of extremly light weight material. It is connected to the battery via a resistance. There is no tension in the supporting wired. The magnetic force only supports the hanging weight.
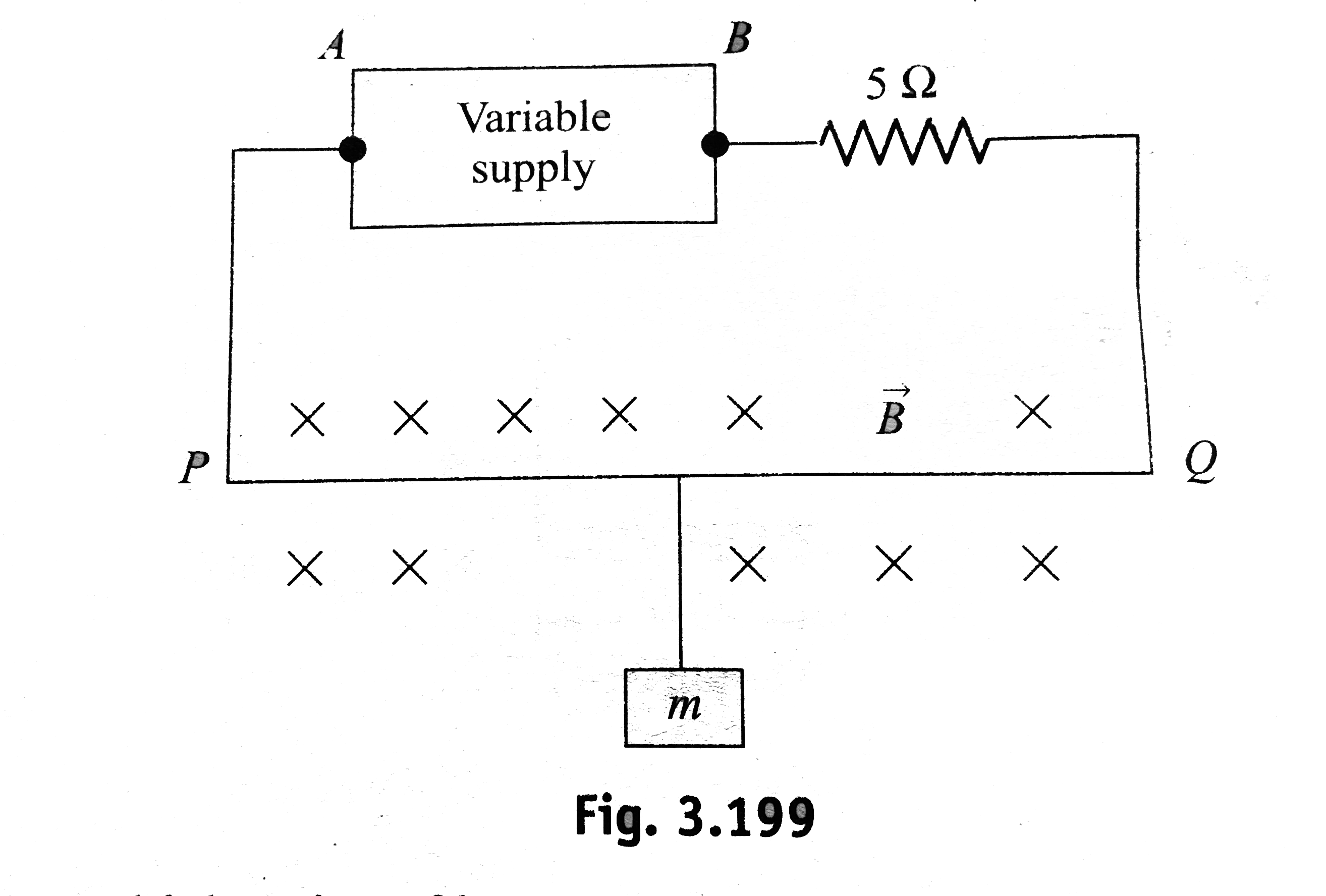
Which point of battery is positive?
View SolutionA block of mass m is placed on a smooth horizontal floor is attached to one end of spring. The other end of the spring is attached to fixed support. When spring is vertical it is relaxed. Now the block is pulled to wards right by a force F, which is being increased gradually. When the speing makes angle 53∘ with the vertical, block leaves the floor.

When blocks leaves the table, the normal force on it from table is
View SolutionA block of mass m is placed on a smooth horizontal floor is attached to one end of spring. The other end of the spring is attached to fixed support. When spring is vertical it is relaxed. Now the block is pulled to wards right by a force F, which is being increased gradually. When the speing makes angle 53∘ with the vertical, block leaves the floor.
When the block leaves the table, the force F is :-
View SolutionA block of mass m is placed on a smooth horizontal floor is attached to one end of spring. The other end of the spring is attached to fixed support. When spring is vertical it is relaxed. Now the block is pulled to wards right by a force F, which is being increased gradually. When the speing makes angle 53∘ with the vertical, block leaves the floor.

Force constant of the spring is :-
View Solution
