The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100m long is supported by vertical wires attached to the cable, the longest wire being 30m and the shortest being 6m. Find the length of the supporting wire attached to the roadway 18m from the middle.
To solve the problem, we will follow these steps:
Step 1: Understand the Geometry of the Problem
The cable of the suspension bridge hangs in the shape of a parabola. The roadway is horizontal and 100 meters long, with the longest supporting wire being 30 meters and the shortest being 6 meters at the center.
Step 2: Identify Key Points
- The center of the roadway is at the origin (0, 0).
- The ends of the roadway are at (-50, 0) and (50, 0) since the total length is 100 meters.
- The shortest wire (6 meters) is at the center (0, 6).
- The longest wires at the ends are at (-50, 30) and (50, 30).
Step 3: Set Up the Parabola Equation
The general form of a parabola that opens upwards is given by:
x2=4ay
We need to find the value of a using the points we have.
Step 4: Use the End Points to Find a
Using the point (50, 30):
502=4a⋅30
2500=120a
a=2500120=62530=1256
Step 5: Write the Parabola Equation
Now substitute a back into the parabola equation:
x2=250030y
or
x2=6256y
Step 6: Find the Length of the Supporting Wire 18m from the Middle
We need to find the length of the supporting wire at x=18 meters from the center:
182=6256y
324=6256y
y=324⋅6625=1944625
Step 7: Calculate the Total Length of the Supporting Wire
The total length of the supporting wire at this point will be:
Length=Shortest wire length+y
=6+1944625
Step 8: Convert to Decimal
Calculating 1944625:
1944625≈3.1104
So,
Length≈6+3.1104=9.1104
Final Answer
The length of the supporting wire attached to the roadway 18 meters from the middle is approximately:
9.11 meters
---
The cable of the suspension bridge hangs in the shape of a parabola. The roadway is horizontal and 100 meters long, with the longest supporting wire being 30 meters and the shortest being 6 meters at the center.
- The center of the roadway is at the origin (0, 0).
- The ends of the roadway are at (-50, 0) and (50, 0) since the total length is 100 meters.
- The shortest wire (6 meters) is at the center (0, 6).
- The longest wires at the ends are at (-50, 30) and (50, 30).
The general form of a parabola that opens upwards is given by:
x2=4ay
We need to find the value of a using the points we have.
Using the point (50, 30):
502=4a⋅30
2500=120a
a=2500120=62530=1256
Now substitute a back into the parabola equation:
x2=250030y
or
x2=6256y
We need to find the length of the supporting wire at x=18 meters from the center:
182=6256y
324=6256y
y=324⋅6625=1944625
The total length of the supporting wire at this point will be:
Length=Shortest wire length+y
=6+1944625
Calculating 1944625:
1944625≈3.1104
So,
Length≈6+3.1104=9.1104
The length of the supporting wire attached to the roadway 18 meters from the middle is approximately:
9.11 meters
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
886 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m. Find t
View SolutionThe cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100m long is supported by vertical wires attached to the cable, the longest wire being 30m and the shortest being 6m. Find the length of which is at 18m apart from the middle point of cable.
View Solutionover the towers of a bridge a cable is hung in the form of a parabola, have their tops 30 meters above the road way are 200 meters apart. If the cable is 5 meters above the road way at the centre of the bridge, then the length of the vertical supporting cable 30 meters from the centre is
View SolutionA lift of mass m is supported by a cable that can with stand a force of 3mg. Find the shortest distance in which the lift can be stopped when it is descending with a speed of g/4.
View SolutionIf the distribution of weight is uniform, then the rope of the suspended bridge takes the form of parabola.The height of the supporting towers is 20m, the distance between these towers is 150m and the height of the lowest point of the rope from the road is 3m. Find the equation of the parabolic shape of the rope considering the floor of the parabolic shape of the rope considering the floor of the bridge as X-axis and the axis of the parabola as Y-axis. Find the height of that tower which supports the rope and is at a distance of 30 m from the centre of the road.
View SolutionA metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
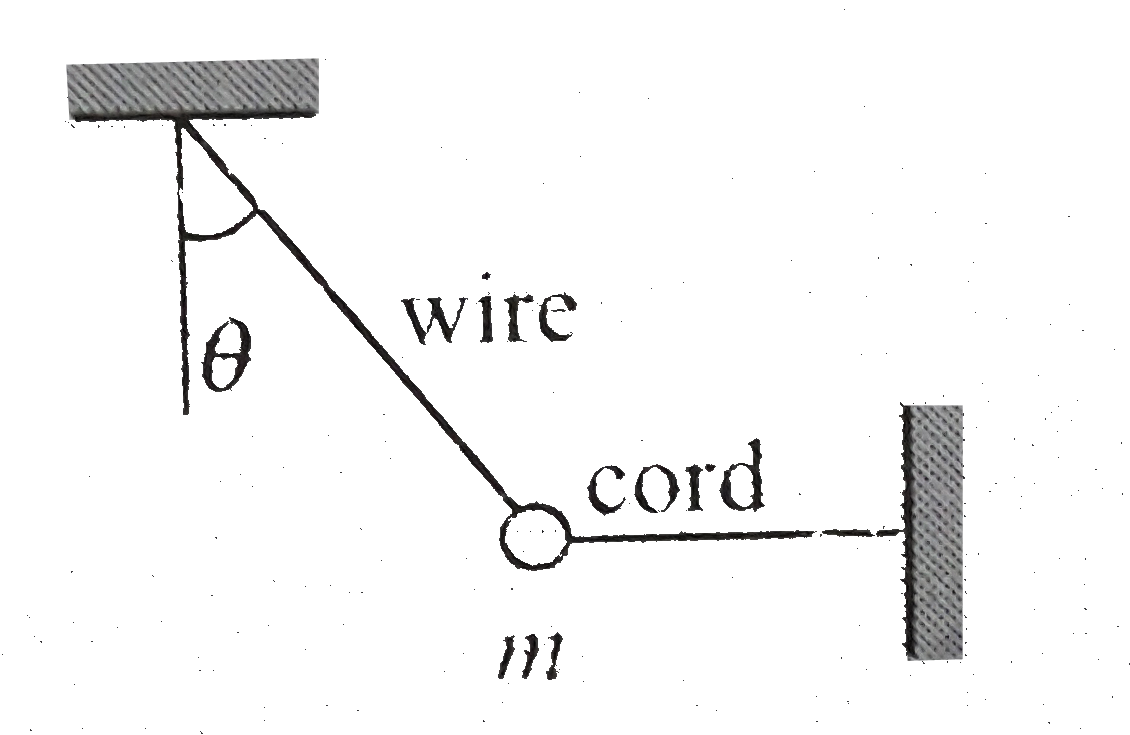
View SolutionA small mass m and its supporting wire because a simple pendulum when the horizontal cord is cut . Find the ratio of the tension in the supporting wire immediately after the cord is cut to the tension in the wire before the cord is cut
View SolutionA particular resistance wire has a resistance of 3.0 ohm per metre. Find :
The total resistance of three lengths of this wire each 1.5 m long, joined in parallel.
View SolutionA rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to
View SolutionA rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to
View Solution
