The center of circle O (not shown) falls on the point where the line y=43x+4 intersects the x-axis on the coordinate plane. The point (3, 8) lies on the circumference of the circle. Which of the following could be the equation for circle O?
x2+y2=25
(x+3)2+y2=25
(x+3)2+y2=100
(x+3)2+(y−8)2=100
The correct Answer is:C
To solve the problem step by step, we need to find the equation of circle O given that its center lies at the intersection of the line y=43x+4 and the x-axis, and that the point (3, 8) lies on the circumference of the circle.
Step 1: Find the intersection point of the line and the x-axis.
The x-axis is represented by the equation y=0. To find the intersection point, we set y in the line equation to 0:
0=43x+4
Step 2: Solve for x.
Rearranging the equation gives:
43x=−4
Multiplying both sides by 34:
x=−3
Step 3: Determine the coordinates of the center of the circle.
Since y=0 at the intersection, the coordinates of the center O are:
(−3,0)
Step 4: Calculate the radius of the circle.
The radius is the distance from the center O(−3,0) to the point on the circumference P(3,8). We use the distance formula:
d=√(x2−x1)2+(y2−y1)2
Substituting the coordinates:
d=√(3−(−3))2+(8−0)2
Step 5: Simplify the expression.
Calculating inside the square root:
d=√(3+3)2+(8)2=√(6)2+(8)2=√36+64=√100=10
Thus, the radius r is 10.
Step 6: Write the equation of the circle.
The general equation of a circle with center (h,k) and radius r is:
(x−h)2+(y−k)2=r2
Substituting h=−3, k=0, and r=10:
(x+3)2+(y−0)2=102
This simplifies to:
(x+3)2+y2=100
Final Equation:
The equation of circle O is:
(x+3)2+y2=100
The x-axis is represented by the equation y=0. To find the intersection point, we set y in the line equation to 0:
Rearranging the equation gives:
Since y=0 at the intersection, the coordinates of the center O are:
The radius is the distance from the center O(−3,0) to the point on the circumference P(3,8). We use the distance formula:
Calculating inside the square root:
The general equation of a circle with center (h,k) and radius r is:
The equation of circle O is:
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the xy-plane, a circle with center O passes through the point (2, 0) and has a radius of 4. Which of the following could be the equation of circle O?
A(x−2)2+(y+4)2=4B(x−2)2+(y+4)2=16C(x−4)2+(y+2)2=16D(x+2)2+(y−2)2=16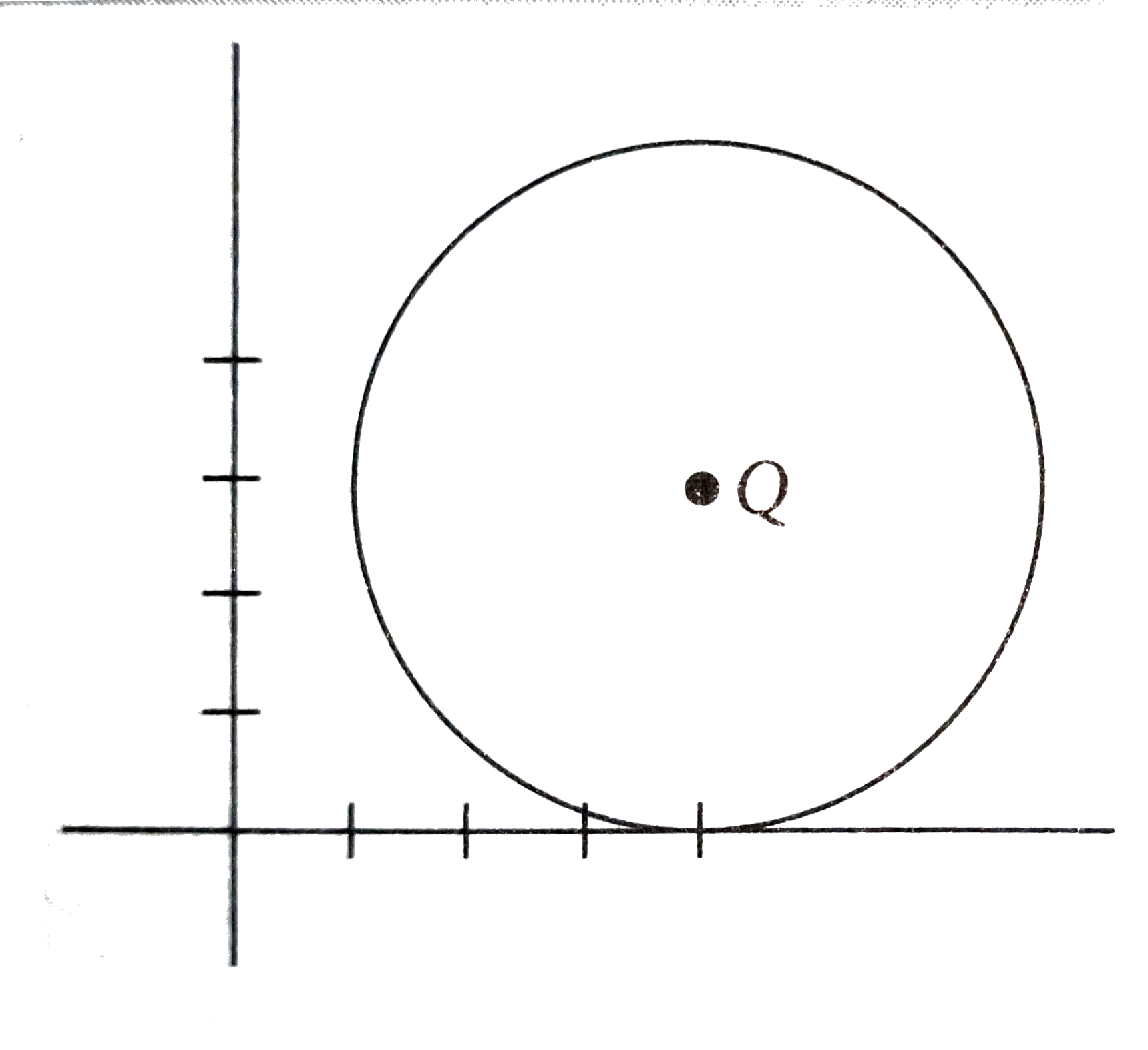
Center Q of the circle above has coordinate of (4,3). What is the circumference of the circle?AπB2πC6πD9πCircle C (not shown) is drawn on a coordinate plane, centered at the origins. If the point (a, b) lies on the circumference of the circle, what is the radius of the cirle in terms of a and b?
Aa−bBa+bC√a2+b2Da2+b2

Point O is the center of the circle above. What fraction of the circumference of the circle is the length of the bolded arc?
View SolutionThe line 2x−y+1=0 is tangent to the circle at the point (2, 5) and the center of the circle lies on x−2y=4 . Then find the radius of the circle.
View SolutionA circle in the stadard (x,y) coordinate plane has center ( 5, -3) and radius 4 units. Which of the following equations represents this circle ?
View Solution
Point P is the certer of the circle shown above, which has a radius of 4. Which of the following points lies on circle P?
View SolutionA circle in the xy-plane is tangent to the x-axis at -10 and the y-axis at 10. Which of the following is an equation of the circle ?
View Solution
