The circle x2+y2=4cuts the line joining the points A(1,0) and B(3,4) in two points P and Q. Let BPPA=α and BQQA=β. Then α and β are roots of the quadratic equation Solution in Tamil
3x2−16x+21=0
x2−8x+7=0
x2−9x+8=0
none of these
The correct Answer is:1
The equation of the line joining A(1,0) and B(3,4) is y=2x−2
This cuts the circle x2+y2=4 at Q(0,−2) and P(8/5,6/5). We have BQ=3√5,QA=√5,BP=7√5 and PA=3√5 . Therefore,
α=BPPA=7√53√5=73
and β=BQQA=3√5√5=3
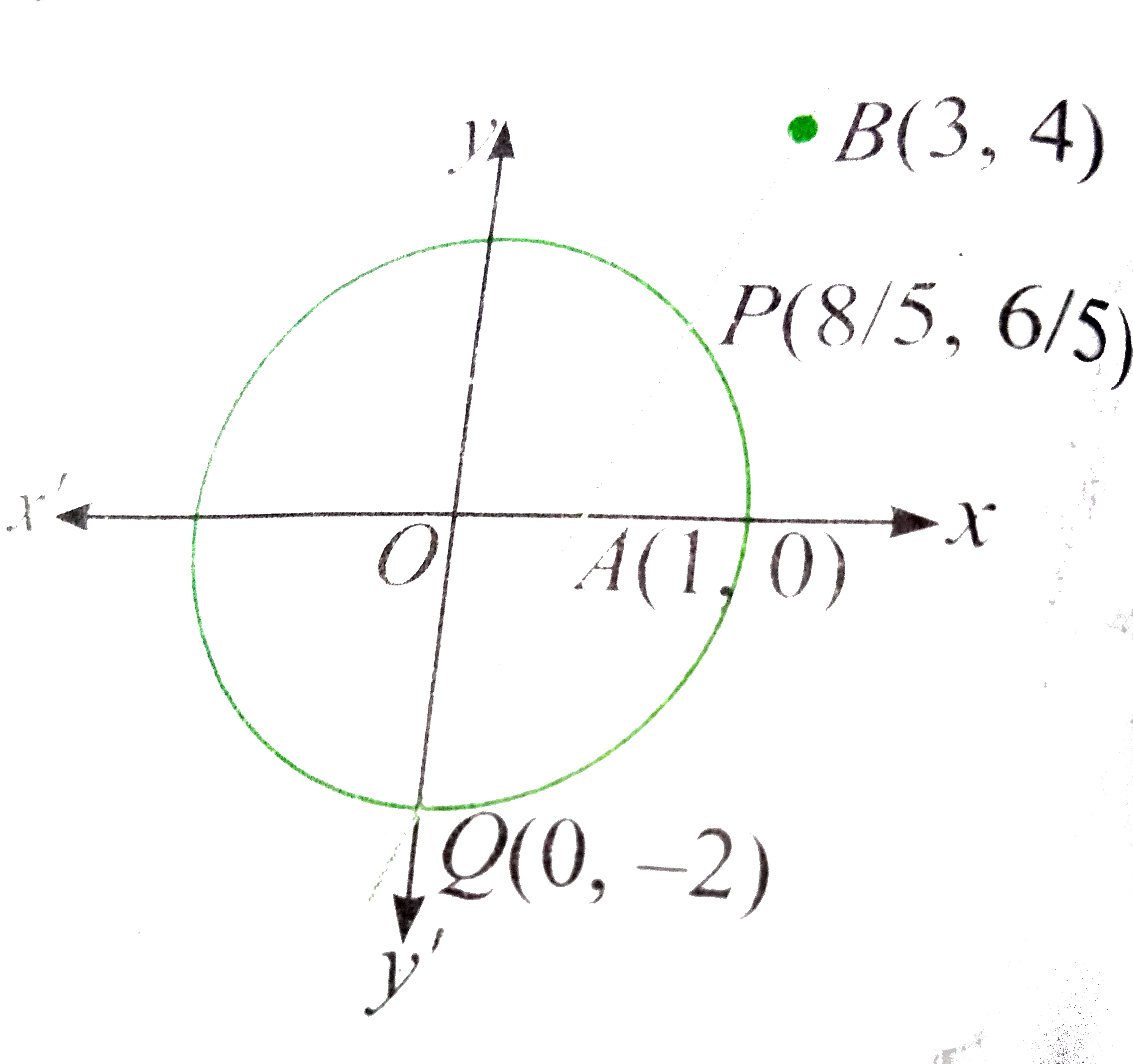
Therefore, α and β are roots of the equation
x2−x(alph+β)+αβ=0
i.e., x2−x(73−3)+73(3)=0
or 3x2−16x+21=0
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
about to only mathematics
View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
View SolutionIf the circle x2+y2+2x+3y+1=0 cuts x2+y2+4x+3y+2=0 at AandB , then find the equation of the circle on AB as diameter.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionIf alpha and beta are the roots of a quadratic equation such that alpha+beta=2,alpha^(4)+beta^(4)=272, then the quadratic equation is
View SolutionIf alpha and beta are the roots of equation x^(2)-4x+13=0, then quadratic equation x^(2)-4x+13=0, then quadratic equation whose root ate alpha^(4)-4 alpha^(3)+13 alpha^(2)+2 and (beta^(3)-4 beta^(2)+13 beta+1)/(4) is
View SolutionThe circle x^(2)+y^(2)=4 cuts the line joining the points A(1,0) and B(3,4) in two points P and Q. Let B(P)/(P)A=alpha and B(Q)/(Q)A=beta. Then alpha and beta are roots of the quadratic equation
View SolutionIf the circles described on the line joining the points (0,1) and (alpha,beta) as diameter cuts the X - axis in points whose abscissae are roots of equation x^(2)-5x+3=0 then (alpha,beta)=
View SolutionIf the roots of the equation x2−px+q=0 be α,β and the roots of the equation x2−ax+b=0 be α,1β then prove that, bq(a−p)2=(q−b)2.
View SolutionLet α,β are the two real roots of equation x2+px+q=0,p,q∈R,q≠0. If the quadratic equation g(x)=0 has two roots α+1α,β+1β such that sum of roots is equal to product of roots, then the complete range of q is:
View Solutionx2+px+q=0 is a quadratic equation, the roots are α,β then α4+β4 is………..
View SolutionIf α,β are the roots of the quadratic equation x2+px+q=0 ,then the values of α3+β3andα4+α2β2+β4 are respectively .
View SolutionThe circle x2+y2=4 ,cuts the line joining the points A(1,0),&B(3,4) in two points P& Q.Let BPPA=α>0&BQQA=β>0 .Then α+β
View SolutionThe circle x2+y2=4cuts the line joining the points A(1,0) and B(3,4) in two points P and Q. Let BPPA=α and BQQA=β. Then α and β are roots of the quadratic equation
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View Solution
