The equation of the line inclined at an angle of π4 to the x-axis ,such that the two circles x2+y2=4 and x2+y2−10x−14y+65=0 intercept equal length on it, is (A) 2x−2y−3=0 (B) 2x−2y+3=0 (C) x−y+6=0 (D) x−y−6=0Solution in Tamil
2x−2y−3=0
2x−2y+3=0
x−y+6=0
x−y−6=0
The correct Answer is:1
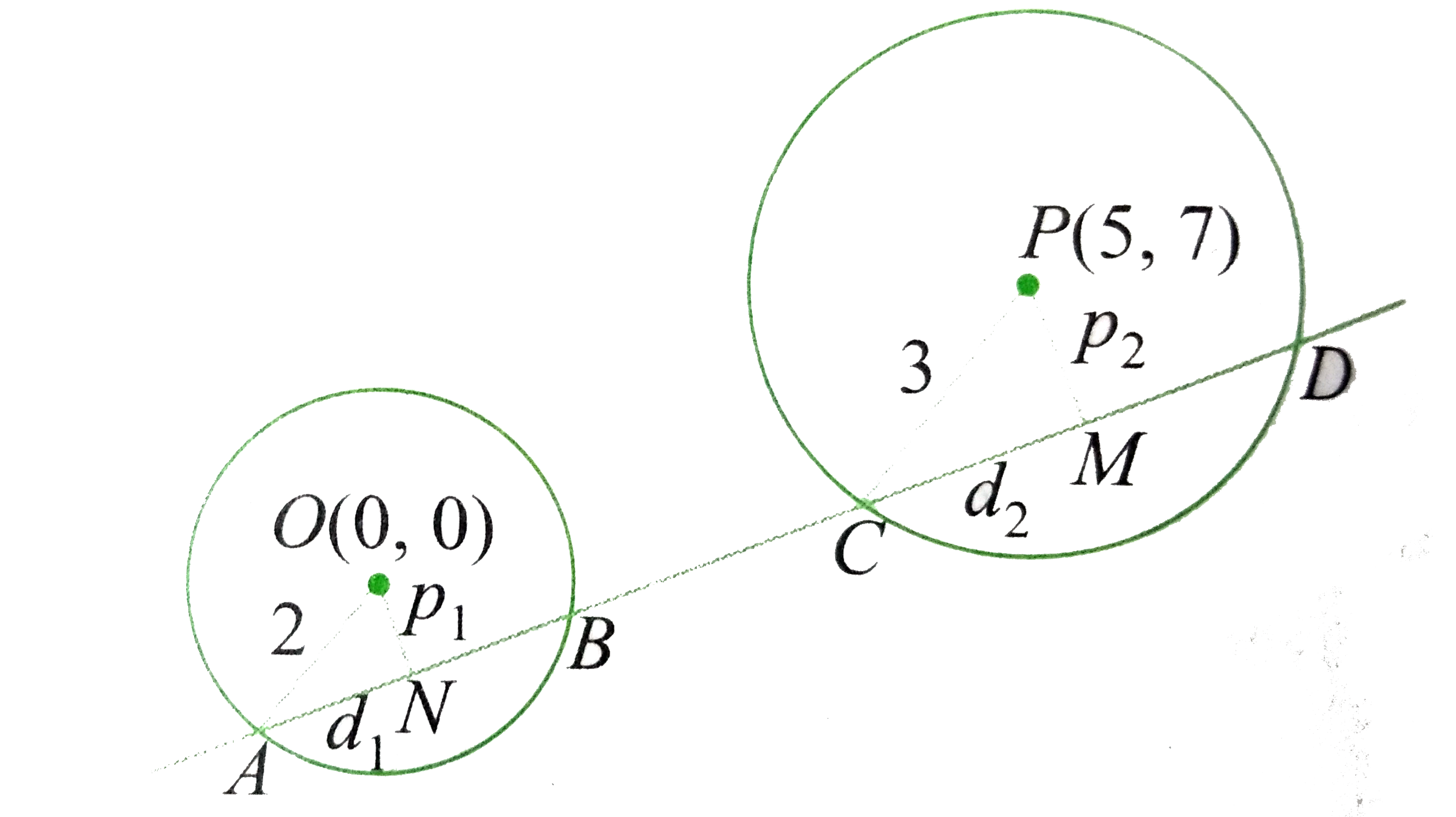
Let the equation of line be
y=x+c or y−x=c
Ther perpendicular from (0,0) on line (1) in ∣∣c/√2∣∣
The perpendicular from (5,7) on line (1) is |c−2|/√2
In ΔAON,
⎷22−(c√2)2=AN
and in ΔCPM
⎷32−(2−c√2)2=CM
Given AN=CM
or 4−c22=9=9−(2−c)22 or c=−32
Therefore, the equation of the line is
y=x−32 or 2x−2y−3=0
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
about to only mathematics
View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
View SolutionIf the circle x2+y2+2x+3y+1=0 cuts x2+y2+4x+3y+2=0 at AandB , then find the equation of the circle on AB as diameter.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionThe lines x+2y+3=0,x+2y−7=0,and2x−y−4=0 are the sides of a square. The equation of the remaining side of the square can be (a) 2x−y+6=0 (b) 2x−y+8=0 (c) 2x−y−10=0 (d) 2x−y−14=0
View SolutionThe equation of the line inclined at an angle of π4 to the x-axis ,such that the two circles x2+y2=4 and x2+y210x−14y+65=0 intercept equal length on it, is (A) 2x−2y−3=0 (B) 2x−2y+3=0 (C) x−y+6=0 (D) x−y−6=0
View SolutionThe shortest distance between the line x+y+10=0 and the circle x^(2)+y^(2)+2x+2y=0 is
View SolutionEquation of the diameter of the circle x^(2)+y^(2)-2x+4y=0 which passes through the origin is x+2y=0 b.x-2y=0 c.2x+y=0 d.2x-y=0
View SolutionThe equation of the normal to the curve y=x(2−x) at the point (2, 0) is x−2y=2 (b) x−2y+2=0 (c) 2x+y=4 (d) 2x+y−4=0
View SolutionIf the lines 2x+3y+1=0 and 3x−y−4=0 lie along diameters of a circle of circumference 10π ,then the equation of the circle is (A) x2+y2−2x+2y−23=0 (B) x2+y2+2x−2y−23=0 (C) x2+y2+2x+2y−23=0 (D) x2+y2−2x−2y−23=0
View Solutionउस वृत्त का समीकरण निकालें जो दिए गए वृत्तों
x2+y2−6x+2y+4=0 तथा x2+y2+2x−4y−6=0 के छेदन-बिंदुओं से जाता है तथा जिसका केंद्र रेखा y=x पर स्थित है।
View SolutionThe lines x+2y+3=0,x+2y−7=0,and2x−y−4=0 are the sides of a square. The equation of the remaining side of the square can be (a) 2x−y+6=0 (b) 2x−y+8=0 (c) 2x−y−10=0 (d) 2x−y−14=0
View SolutionThe equation of the line inclined at an angle of π4 to the x-axis ,such that the two circles x2+y2=4 and x2+y210x−14y+65=0 intercept equal length on it, is (A) 2x−2y−3=0 (B) 2x−2y+3=0 (C) x−y+6=0 (D) x−y−6=0
View SolutionThe lines x+2y+3=0,x+2y−7=0,and2x−y−4=0 are the sides of a square. The equation of the remaining side of the square can be 2x−y+6=0 (b) 2x−y+8=0 2x−y−10=0 (b) 2x−y−14=0
View SolutionThe equation of the normal to the curve y=x(2−x) at the point (2, 0) is
(a)x−2y=2
(b) x−2y+2=0
(c) 2x+y=4
(d) 2x+y−4=0
View Solution
