The circles in the figure are of equal radii and cu at points L and M. If the distance between the centres O1andO2 is 8 cm and the radius is 5 cm, find LM.
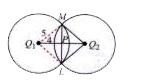
The correct Answer is:6 cm
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - TEST YOURSELF (LEVEL 2)
7 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - TEST YOURSELF (LEVEL 3)
8 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
6 Videos
- ALGEBRAIC EXPRESSIONS AND POLYNOMIALS BOOK - CENGAGECHAPTER - ALGEBRAIC EXPRESSIONS AND POLYNOMIALS EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
- LAWS OF EXPONENTS AND LOGARITHMS BOOK - CENGAGECHAPTER - LAWS OF EXPONENTS AND LOGARITHMS EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
Similar Questions
Knowledge Check
Two circles of radii 13 cm and 5 cm touch internally each other. Find the distance between their centres:
A18 cmB12 cmC9 cmD8 cmTwo circles of radii 13 cm and 5 cm touch internally each other. Find the distance between their centres:
A18 cmB12 cmC9 cmD8 cmThe length of the direct common tangent of two circles of radii 2 cm and 8 cm is 8 cm. Then the distance between the centres of the circles is
A8 cmB10 cmC6 cmD12 cm
Two circles with radii 5 cm and 4.5 cm touch each other externally then find the distance between their centre.
View SolutionTwo circles of radii 5 cm and 3cm intersect at two points and the distance between their centres is 4cm. Find the length of the common chord.
Let the common chord be AB and Pand Q be the centers of the two circles.
AP=5cmand AQ=3cm.
PQ=4cm ...given
Now, segPQ⊥chordAB
AR=RB=12AB....perpendicular from center to the chord, bisects the chord
Let PR=xcm
so RQ=(4−x)cm
In△ARP,AP2=AR2+PR2
AR2=52−x2...(1)
In △ARQ,AQ2=AR2+QR2
AR2=32−(4−x)2...(2)
52−x2=32−(4−x)2...from (1) & (2)
25−x2=9−(16−8x+x2)
25−x2=−7+8x−x2
32=8x
x=4 substituting in equation(1) we get , AR2=25−16=9
AR=3cm
AB=2×AR=2×3=6
AB=6cmSo length of common chord is6 cm.
View SolutionTwo circles having radii 3.5 cm and 4.8 cm touch each other internally. Find the distance between thir centres.
View SolutionIf two circles with radii 5 cm and 3 cm respectively touch internally, find the distance between their centres.
View SolutionIf two circles with radii 8 cm and 3 cm respectively touch externally, then find the distance between their centres.
View Solution