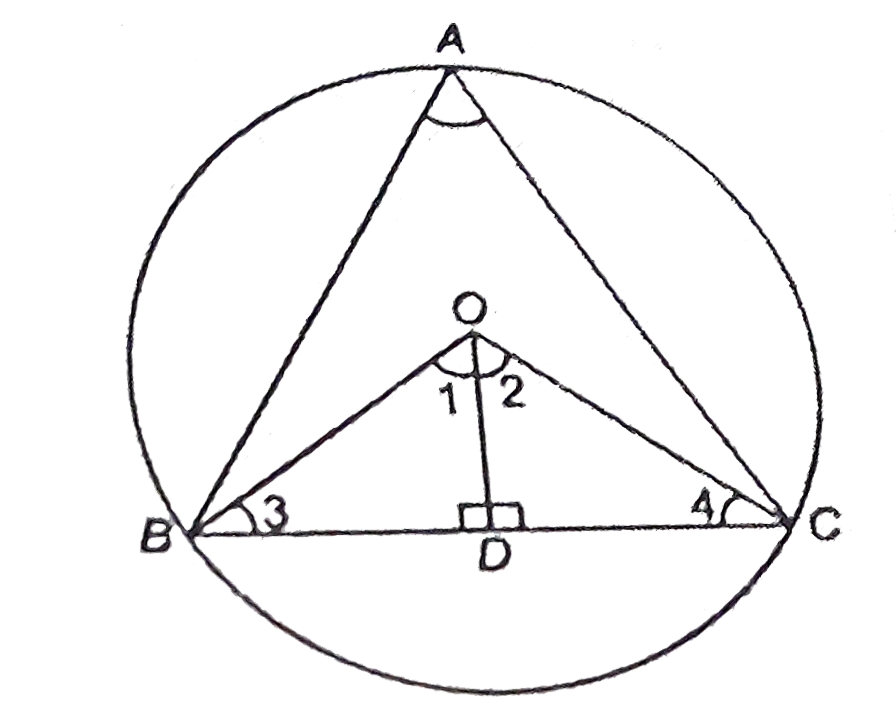
The circumcentre of the triangle ABC is O . Prove that $∠ O B C + ∠ B A C = 90^{\circ}$ .

Video Solution

Text Solution

Verified by Experts

ABC is a triangle and O is its circumcentre.
Draw $O d ⊥ B C$ . Join OB and OC.
In right $Δ O B D$ and right $Δ O C D$ , we have
hypotenuse OB=hyotenuse OC radii of the same circle)
$O D = O D$ (common side)
$∴ Δ O B D ≅ Δ O C D$ (by R.H.S. congruency rule)
$∴ ∠ 1 = ∠ 2$ and $∠ 3 = ∠ 4$ (c.p.c.t)
Now, $∠ B O C = 2 ∠ 1$ and $∠ B O C = 2 ∠ A$
$∴ 2 ∠ 1 = 2 ∠ \Rightarrow ∠ 1 = ∠ A$
$∴ ∠ A = ∠ 2$
$(∵ ∠ 1 = ∠ 2)$ ........(1)
$\Rightarrow ∠ A + ∠ 3 = 90^{\circ} (∵ ∠ 2 + ∠ 4 = 90^{\circ} and ∠ 4 = ∠ 3)$
$\Rightarrow ∠ O B C + ∠ A = 90^{\circ}$ .

Updated on:21/07/2023

The circum-centre of a triangle ABC is O. If $∠ B A C = 85^{\circ}$ , $∠ B C A = 75^{\circ}$ , then $∠ O A C$ is of
A $70^{\circ}$
B $72^{\circ}$
C $75^{\circ}$
D $74^{\circ}$
O is the circumcentre of the triangle ABC and $∠ B A C = 85^{\circ}$ , $∠ B C A = 75^{\circ}$ , then the value of $∠ O A C$ is
A $55^{\circ}$
B $150^{\circ}$
C $20^{\circ}$
D $70^{\circ}$
If O is the circumcentre of a triangle ABC lying inside the tri angle, then $∠ O B C + ∠ B A C$ is equal to
A $90^{\circ}$
B $60^{\circ}$
C $110^{\circ}$
D $120^{\circ}$