If O is the circumcenter of △ABC and ∠OBC=35∘, then the ∠BAC is equal to
यदि O, △ABC का परिकेन्द्र है और ∠OBC=35∘ तो ∠BAC बराबर है-
55∘
110∘
70∘
35∘
To solve the problem, we need to determine the angle ∠BAC given that O is the circumcenter of triangle ABC and ∠OBC=35∘.
1. Understanding the Circumcenter:
The circumcenter O of triangle ABC is the point where the perpendicular bisectors of the sides of the triangle intersect. It is also the center of the circumcircle that passes through the vertices A, B, and C.
2. Identifying the Angles:
We are given that ∠OBC=35∘. Since O is the circumcenter, the segments OB and OC are radii of the circumcircle.
3. Isosceles Triangle:
Since OB=OC (both are radii of the circumcircle), triangle OBC is an isosceles triangle. Therefore, the angles opposite to the equal sides are also equal:
∠OCB=∠OBC=35∘
4. Finding the Third Angle in Triangle OBC:
The sum of the angles in triangle OBC is 180∘:
∠OBC+∠OCB+∠BOC=180∘
Substituting the known values:
35∘+35∘+∠BOC=180∘
70∘+∠BOC=180∘
∠BOC=180∘−70∘=110∘
5. Using the Inscribed Angle Theorem:
The angle ∠BAC is an inscribed angle that subtends the arc BC. According to the inscribed angle theorem, the measure of an inscribed angle is half the measure of the central angle that subtends the same arc:
∠BAC=12∠BOC
Substituting the value we found:
∠BAC=12×110∘=55∘
Final Answer:
Thus, the angle ∠BAC is equal to 55∘.
---
The circumcenter O of triangle ABC is the point where the perpendicular bisectors of the sides of the triangle intersect. It is also the center of the circumcircle that passes through the vertices A, B, and C.
We are given that ∠OBC=35∘. Since O is the circumcenter, the segments OB and OC are radii of the circumcircle.
Since OB=OC (both are radii of the circumcircle), triangle OBC is an isosceles triangle. Therefore, the angles opposite to the equal sides are also equal:
∠OCB=∠OBC=35∘
The sum of the angles in triangle OBC is 180∘:
∠OBC+∠OCB+∠BOC=180∘
Substituting the known values:
35∘+35∘+∠BOC=180∘
70∘+∠BOC=180∘
∠BOC=180∘−70∘=110∘
The angle ∠BAC is an inscribed angle that subtends the arc BC. According to the inscribed angle theorem, the measure of an inscribed angle is half the measure of the central angle that subtends the same arc:
∠BAC=12∠BOC
Substituting the value we found:
∠BAC=12×110∘=55∘
Thus, the angle ∠BAC is equal to 55∘.
Topper's Solved these Questions
Similar Questions
If I is the incentre of △ABC and ∠BIC=135∘, then △ABC is
यदि I त्रिभुज △ABC का अंतः केंद्र है और ∠BIC=135∘ तो △ABC है-
View SolutionIf ‘'O’ is the orthocenter of the △ABC and ∠BAC=80∘, then the measure of ∠BOC is :-
यदि त्रिभुज ABC का लम्ब केन्द्र 'O' है तथा ∠BAC=80∘ है, तो ∠BOC का माप है।
View Solution
Knowledge Check
O is the circumcentre of the △ABC. If ∠BAC=50∘, then ∠OBC is equal to
A30∘B60∘C40∘D50∘If O is the incentre of a triangle ABC and ∠AOC=124∘, find the ∠ABC.
A56B112C68Dcan't be determinedIn Δ ABC, O is the circum centre of the circle. If ∠OBC=37∘ then ∠BAC is equal to :
A74∘B106∘C53∘D37∘
If L is the circumcentre of △XYZ and angle X is 40∘, then the value of ∠YZL is:
यदि L, XYZ का परिकेंद्र है और ∠X=40∘ है,तब ∠YZL का मान है:
View Solution‘O' is the orthocentre of △ABC.Then ∠BOC+∠BAC is equal to:
O, △ABC में, △ABC का लंबकेंद्र है, तो ∠BOC+∠BAC कितना होगा?
View SolutionIn the given figure, O is the centre of the circle. If ∠BAO=30∘ and ∠BCO=50∘, then ∠AOC is equal to:
दिए गए आकृति में, O वृत्त का केंद्र है। यदि ∠BAO=30∘ और ∠BCO=50∘, तो ∠AOC का मान है :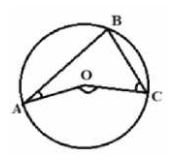
View SolutionIf O is the circumcentre of a triangle ABC lying inside the tri angle, then ∠OBC+∠BAC is equal to
View SolutionO is the circumcentre of the triangle ABC and ∠BAC=85∘, ∠BCA=75∘ , then the value of ∠OAC is
View Solution
