The coordinates of the endpoints of ¯¯¯¯¯¯¯GH, in the standard (x,y) coordinate plane, are (-8, -3) and (2,3). What is the x-coordinate of the midpoint of ¯¯¯¯¯¯¯GH?
−6
−3
0
3
To find the x-coordinate of the midpoint of the line segment ¯¯¯¯¯¯¯¯¯GH with endpoints at coordinates G(−8,−3) and H(2,3), we can follow these steps:
Step 1: Identify the coordinates of the endpoints
The coordinates of point G are (−8,−3) and the coordinates of point H are (2,3).
Step 2: Use the midpoint formula
The formula for finding the midpoint M(x,y) of a line segment with endpoints (x1,y1) and (x2,y2) is given by:
M(x,y)=(x1+x22,y1+y22)
Step 3: Substitute the coordinates into the formula
Here, we have:
- x1=−8
- x2=2
- y1=−3
- y2=3
Now we can calculate the x-coordinate of the midpoint:
Mx=x1+x22=−8+22
Step 4: Simplify the expression
Calculating the numerator:
−8+2=−6
Now, divide by 2:
Mx=−62=−3
Step 5: Conclusion
The x-coordinate of the midpoint M is −3.
Final Answer
The x-coordinate of the midpoint of ¯¯¯¯¯¯¯¯¯GH is −3.
---
The coordinates of point G are (−8,−3) and the coordinates of point H are (2,3).
The formula for finding the midpoint M(x,y) of a line segment with endpoints (x1,y1) and (x2,y2) is given by:
M(x,y)=(x1+x22,y1+y22)
Here, we have:
- x1=−8
- x2=2
- y1=−3
- y2=3
Mx=x1+x22=−8+22
Calculating the numerator:
−8+2=−6
Now, divide by 2:
Mx=−62=−3
The x-coordinate of the midpoint M is −3.
The x-coordinate of the midpoint of ¯¯¯¯¯¯¯¯¯GH is −3.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Which of the following is the equation of a circle in the standard (x,y) coordinate plane ?
A(x-3)+(y+6)=100By=x2+25Cx2=y2+25Dx2=36−y2Point C ( 1,2) and point D ( 7,10) lie in the standard coordiant plane . What are the coordinates of the midpoints of ¯¯¯¯¯¯CD
A(1,8)B(3,−6)C(4,−4)D(4,−6)In the standard (x,y) coordinate plane, what is the slope of the line 3x+8y=5?
A−3B−38C35D3
In the standard (x, y) coordinate plane, what is the slope of the line segement joining the points (3, -5) and (7, 2) ?
View SolutionIn the standard (x,y) coordinate plane, the circle centerd at (1,3) that passes through (4,7) is the set of all points that are:
View SolutionThe slope of a line in the standard (x,y) coordinate plane is 4. What is the slope of a line perpendicular to that line ?
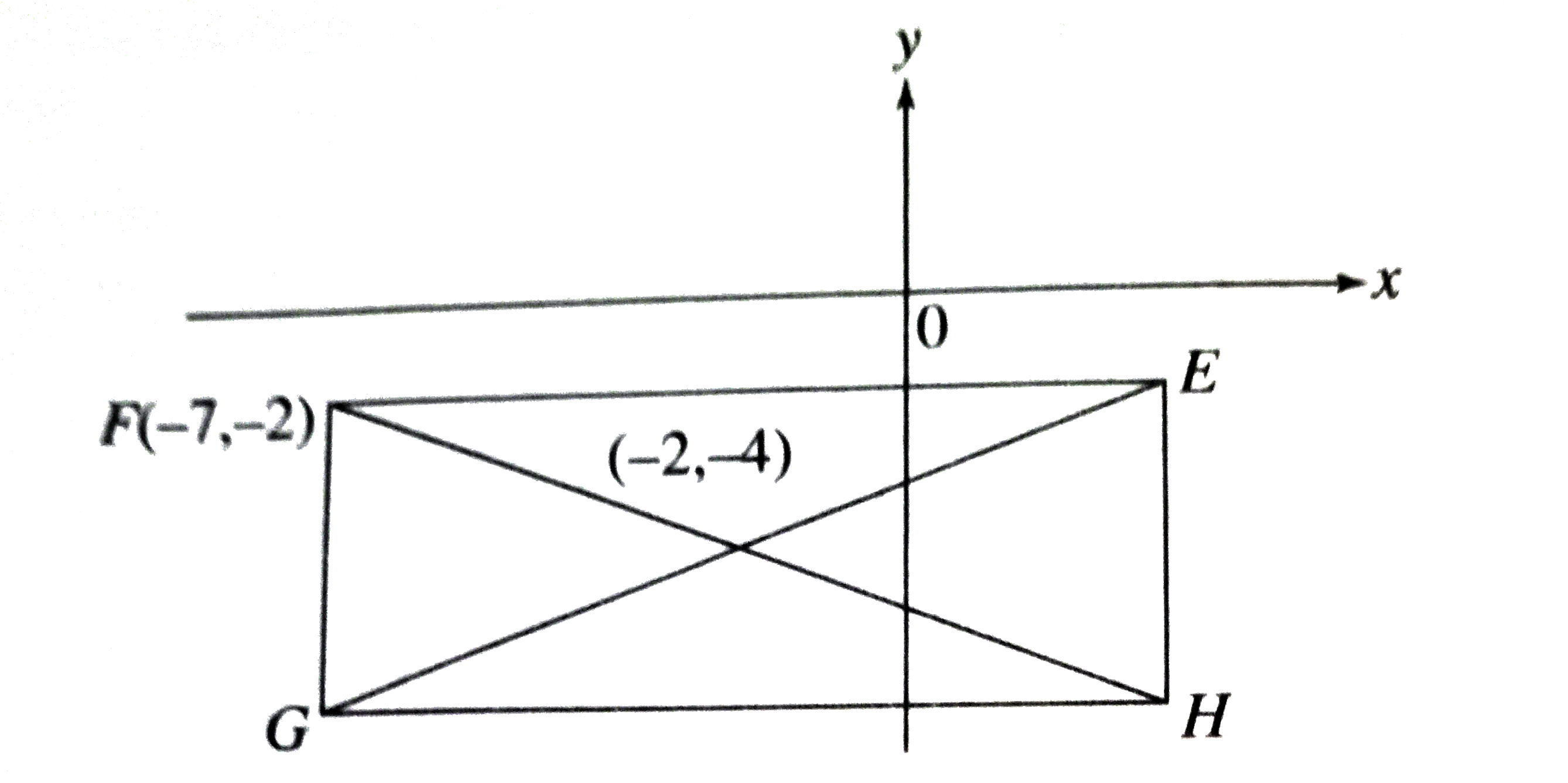
View SolutionAs shown below, the diagonals of rectange EFGH intersect at the point (-2,-4) in the standard (x,y) coordinate plane. Point F is at (-7,-2) . Which of the following are the coordinates of H ?
View SolutionThe point (24,3) on a standard (x,y) coordinate plane is halfway between points (z,2x+1) and (15z,z-4) . What is the value of z ?
View Solution