If the coordinates of the endpoints of a diagonal of square are (−2,−3)and(5,4), what is the number of square units in the area of the square?
The correct Answer is:49
To find the area of the square given the coordinates of the endpoints of its diagonal, we can follow these steps:
Step 1: Identify the coordinates of the endpoints
The endpoints of the diagonal of the square are given as:
- Point A: (-2, -3)
- Point B: (5, 4)
Step 2: Use the distance formula to find the length of the diagonal
The distance d between two points (x1,y1) and (x2,y2) is given by the formula:
d=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of points A and B:
d=√(5−(−2))2+(4−(−3))2
=√(5+2)2+(4+3)2
=√(7)2+(7)2
=√49+49
=√98
=7√2
Step 3: Relate the diagonal to the side of the square
For a square, the relationship between the length of the diagonal d and the side length s is given by:
d=s√2
Setting this equal to the diagonal we found:
7√2=s√2
Step 4: Solve for the side length s
Dividing both sides by √2:
s=7
Step 5: Calculate the area of the square
The area A of a square is given by:
A=s2
Substituting the value of s:
A=72=49
Final Answer
The area of the square is 49 square units.
---
The endpoints of the diagonal of the square are given as:
- Point A: (-2, -3)
- Point B: (5, 4)
The distance d between two points (x1,y1) and (x2,y2) is given by the formula:
d=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of points A and B:
d=√(5−(−2))2+(4−(−3))2
=√(5+2)2+(4+3)2
=√(7)2+(7)2
=√49+49
=√98
=7√2
For a square, the relationship between the length of the diagonal d and the side length s is given by:
d=s√2
Setting this equal to the diagonal we found:
7√2=s√2
Dividing both sides by √2:
s=7
The area A of a square is given by:
A=s2
Substituting the value of s:
A=72=49
The area of the square is 49 square units.
Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE
45 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Multiple Choice
99 Videos
- ADDITIONAL TOPICS IN MATH BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST
24 Videos
- COMPLEX NUMBERSBOOK - ENGLISH SATCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE
6 Videos
Similar Questions
Knowledge Check
If the end points of the diagonal of a square are (-2,3,1) and (-3,5,2) , then the length of the side of the square is
A√2 unitsB√3 unitsC√6 unitsD2√3 units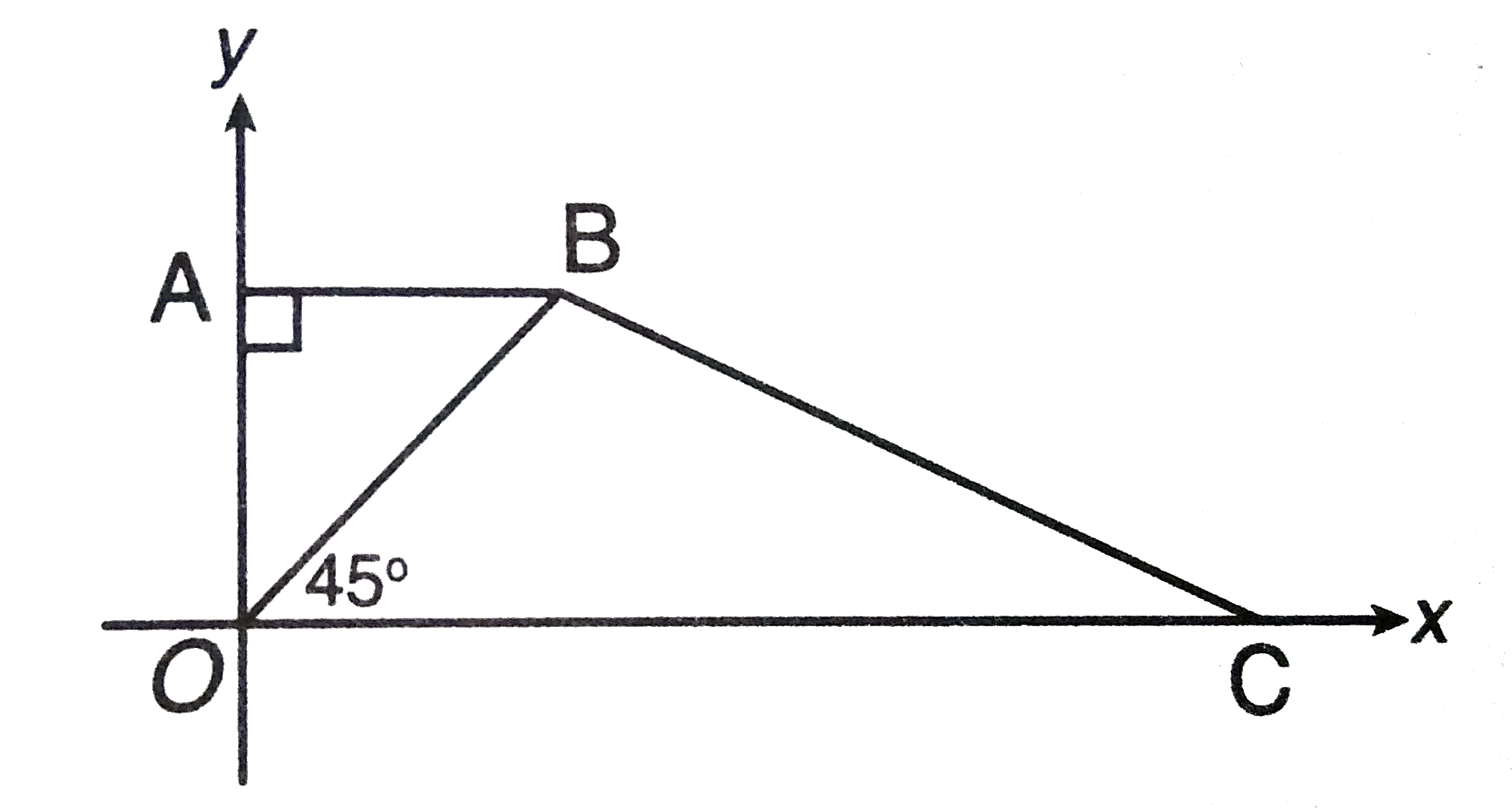
In the figure above, ¯¯¯¯¯¯OA⊥¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ABandm∠BOC=45∘. If the coordinates of point A are (0,3) and the coordinates of point C are (7,0), what is the number of square units in the area of qudrilateral OABC?A15B20C25D30If in the accompanying figure the length of arc AB of circle O is 8π, what is the number of square units in the area of the shaded region?
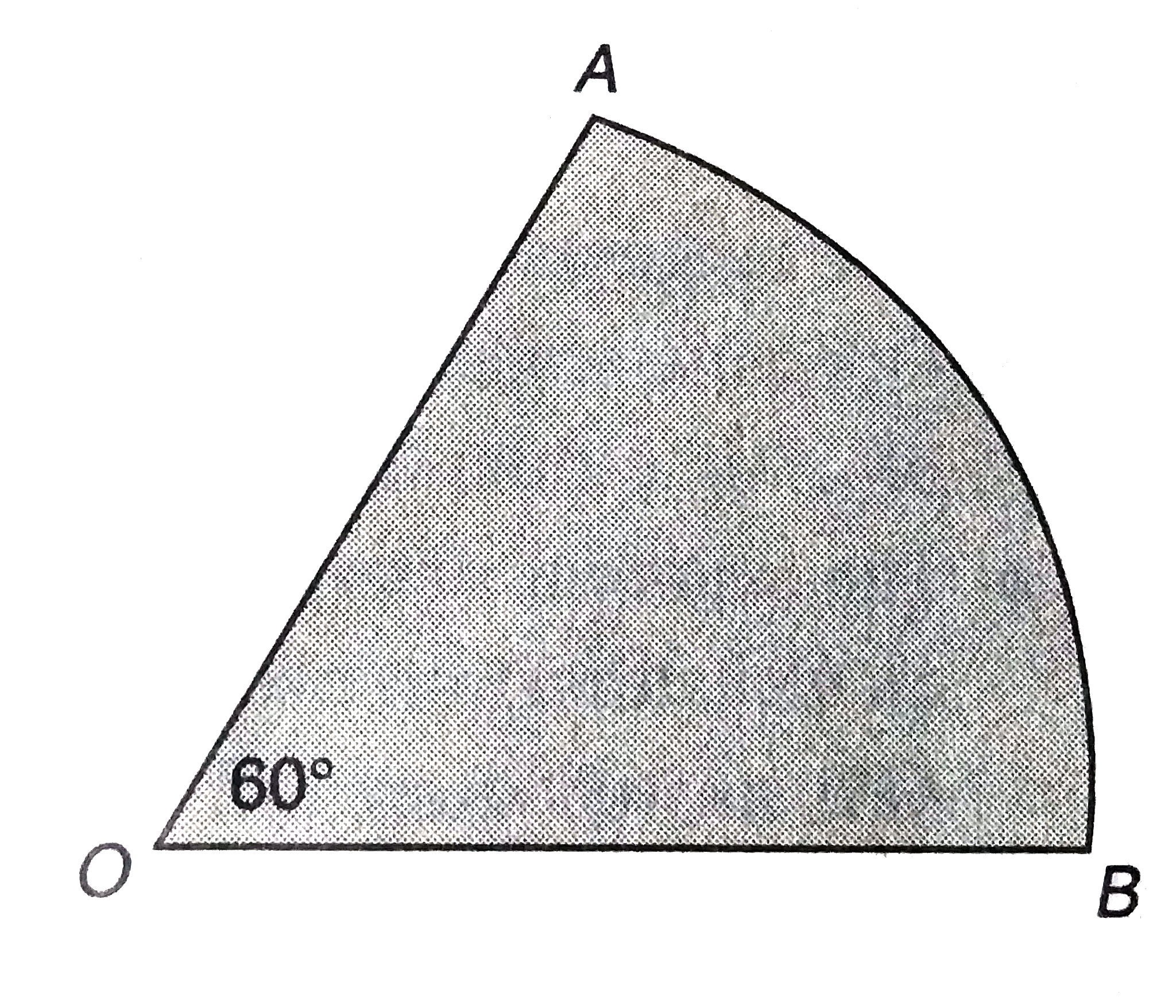 A16πB32πC64πD96π
A16πB32πC64πD96π
What is the diagonal of a square with an area of 25?
View SolutionThe vertices of a diagonal of a square are (−2,4) and (−2,−2) Find the other vertices
View SolutionWhat is the area of a square with diagonal of 6?
View Solution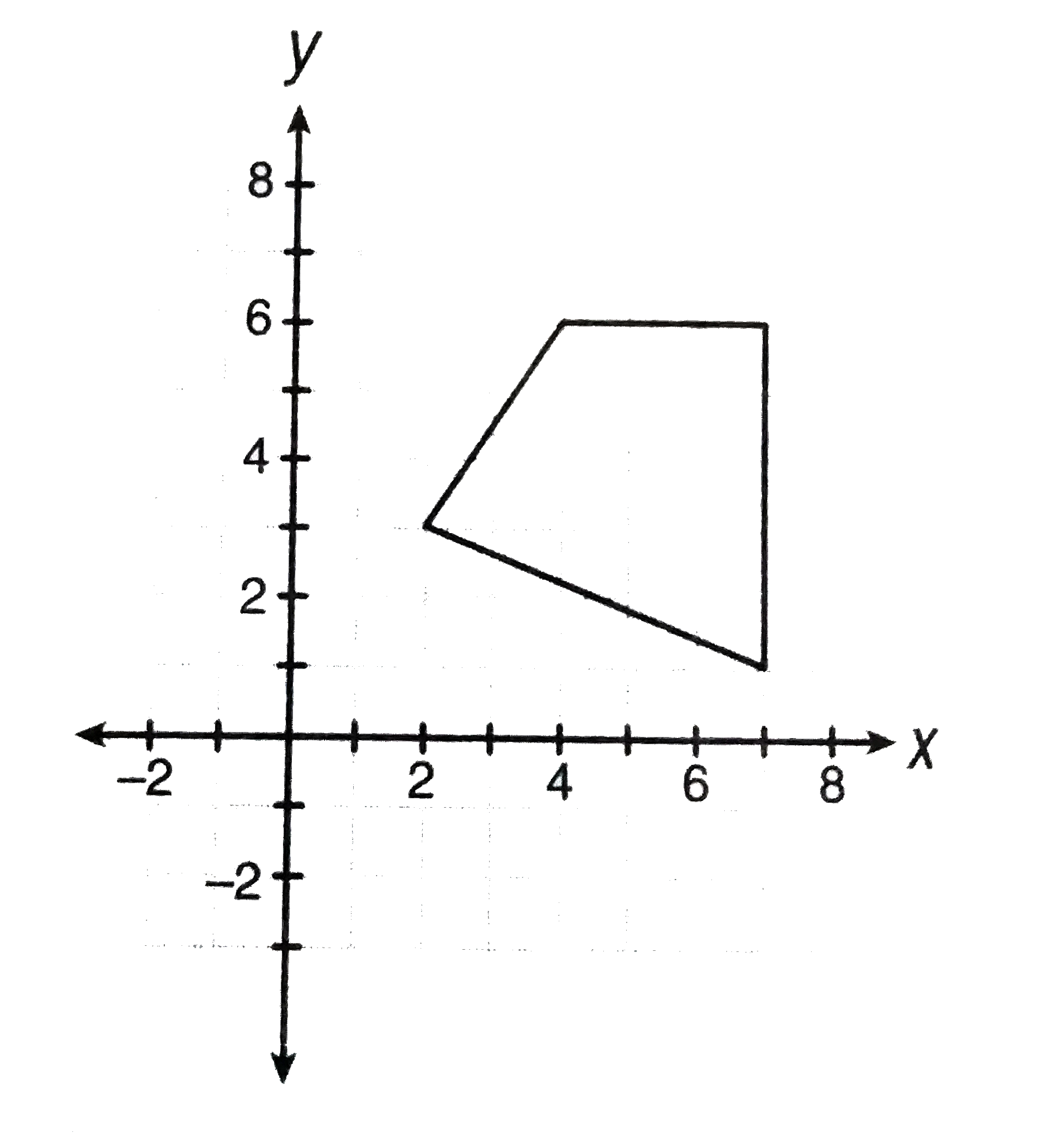
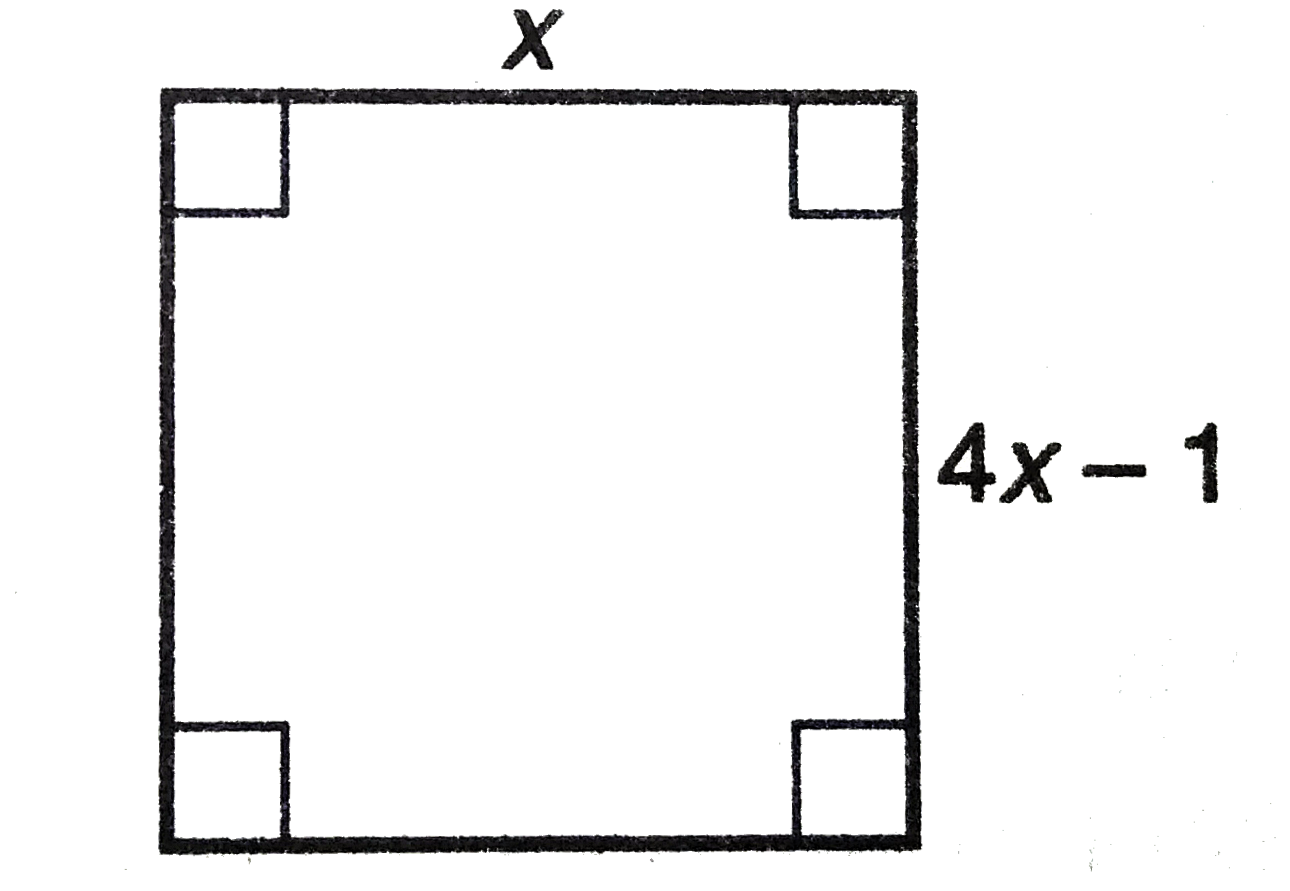
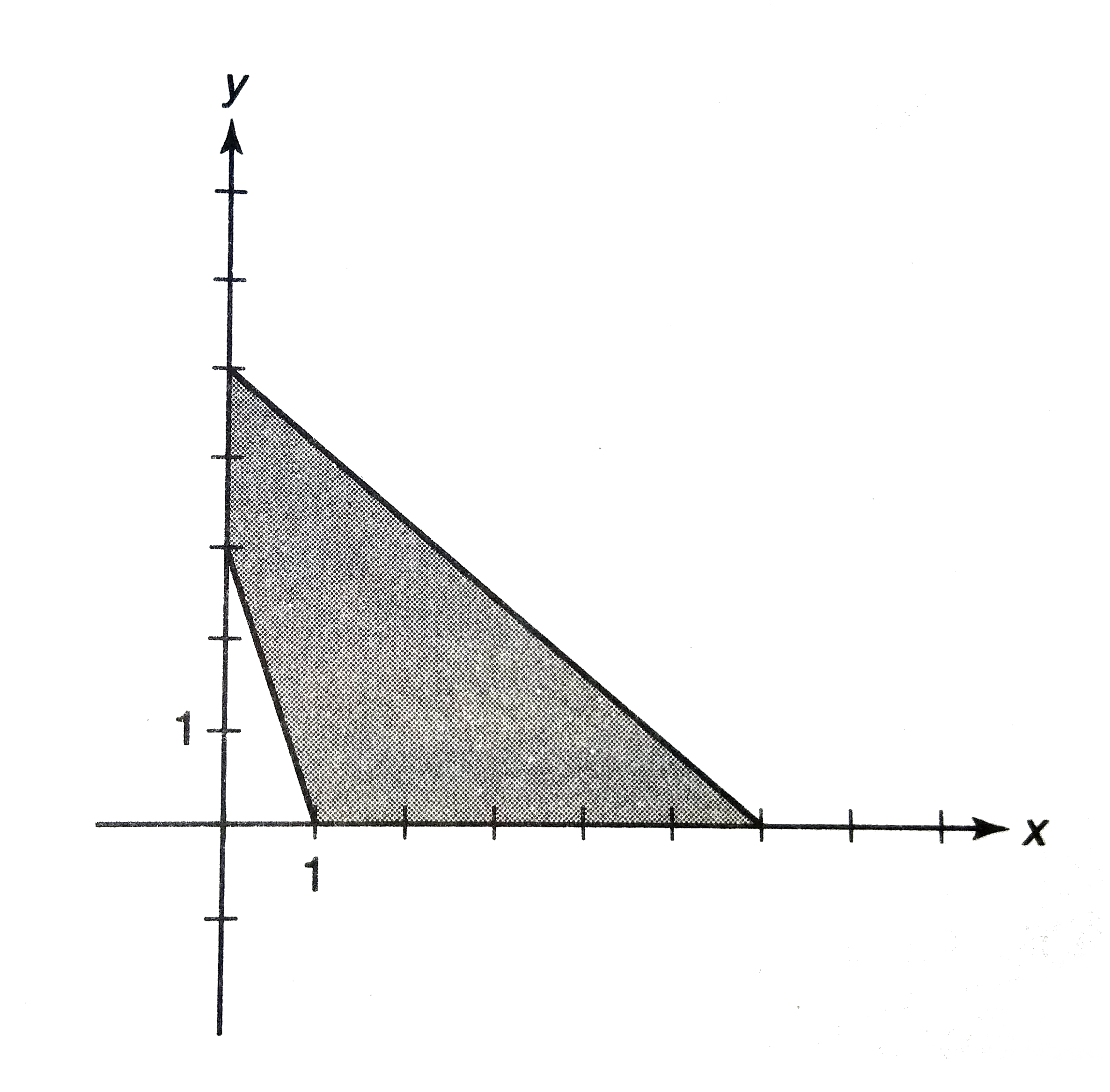
what is the number of square units in the area of the quandrilateral shown in the figure above?
View SolutionThe ends of a diagonal of a square have co-ordinates (−2,p)and(p,2). Find p, if the area of the square is 40 sq. units.
View Solution