The coordinates of the foot of the perpendicular drawn from the origin to the line joining the point (−9,4,5) and (10,0,−1) will be
(-3,2,1)
(1,2,2,)
(4,5,3)
none of these
The correct Answer is:D
Let AD be the perpendicular and D be the foot of the perpendicular which divides BC in the ratio λ:1, then
D(10λ−9λ+1,4λ+1,−λ+5λ+1) (i)
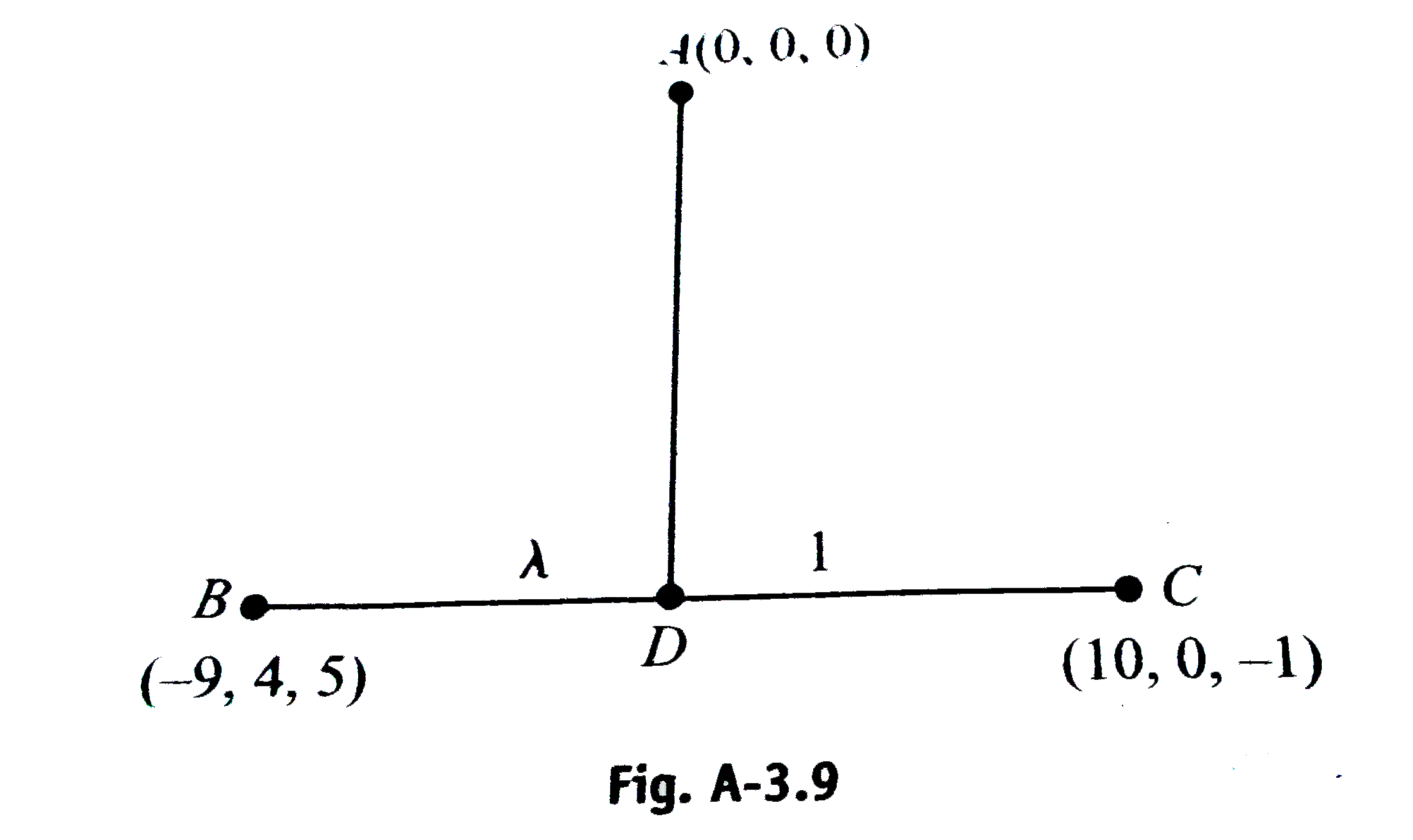
The direction ratio of AD are 10λ−0λ+1,4λ+1and−λ+5λ+1 and direction ratios of BC are 19,-4 and -6.
Since AD⊥BC, we get
19(10λ−9λ+1)−4(4λ+1)−6(−λ+5λ+1)=0
or λ=3128
Hence, on putting the value of λ in (i) ,we get required foot of the perpendicular, i.e., (5859,11259,10959).
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Multiple)
17 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Reasoning Questions)
10 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Subjective)
16 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
20 Videos
- TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank
34 Videos
Similar Questions
The coordinates o the foot of the perpendicular drawn from the origin to the line joining the point (−9,4,5)and(10,0,−1) will be a. (−3,2,1) b. (1,2,2) c. 4,5,3 d. none of these
View SolutionFind the coordinates of the foot of the perpendicular drawn from the point A(−1,8,4) to the line joining the points B(0,−1,3) and C(2,−3,−1).
View Solution
Knowledge Check
The coordinates of the foot of the perpendicular drawn from the origin to the plane 2x−3y+4z−6=0 is
A(12√29,−18√29,24√29)B(18√29,−12√29,24√29)C(1229,−1829,2429)D(1211,−1811,2411)The coordinates of the foot of perpendicular drawn from the origin to the plane 2x+y-2z=18 are ……
A(4,2,4)B(-4,2,4)C(-4,-2,4)D(4,2,-4)The coordinates of the foot of the perpendicular drawn from the point (3,4) on the line 2x+y−7=0 are
A(95,175)B(1,5)C(-5, 1)D(1, -5)
Find the coordinates of the foot of perpendicular drawn from origin to the planes: 5y+8=0
View SolutionFind the coordinates of the foot of the perpendicular drawn from the origin to the plane 3y+4z−6=0.
View SolutionFind the coordinates of the foot of perpendicular drawn from origin to the planes: x+y+z=1
View SolutionFind the coordinates of the foot of the perpendicular drawn from the point A(1,2,1) to the line joining B(1,4,6)andC(5,4,4).
View SolutionFind the coordinates of the foot of perpendicular drawn from th point A(1,8,4) to the line joining the points B(0,−1,3)and C(2−3,−1).
View Solution