The corneer points of a feasible region, determined by a system of linear inequations, are (0,0),(1,0),(4,3),(2,1)and(0,1). If the objective function is Z=2x−3y, then the minimum value of Z is :
−4
−2
−6
−5
To find the minimum value of the objective function Z=2x−3y at the given corner points of the feasible region, we will evaluate Z at each corner point.
1. Identify the corner points: The corner points given are:
- A(0,0)
- B(1,0)
- C(4,3)
- D(2,1)
- E(0,1)
2. Calculate Z at each corner point:
- At point A(0, 0):
Z=2(0)−3(0)=0
- At point B(1, 0):
Z=2(1)−3(0)=2−0=2
- At point C(4, 3):
Z=2(4)−3(3)=8−9=−1
- At point D(2, 1):
Z=2(2)−3(1)=4−3=1
- At point E(0, 1):
Z=2(0)−3(1)=0−3=−3
3. Compare the values of Z:
- Z(A)=0
- Z(B)=2
- Z(C)=−1
- Z(D)=1
- Z(E)=−3
4. Determine the minimum value:
The minimum value of Z occurs at point E(0,1) where Z=−3.
Conclusion:
The minimum value of Z is −3.
---
- A(0,0)
- B(1,0)
- C(4,3)
- D(2,1)
- E(0,1)
- At point A(0, 0):
Z=2(0)−3(0)=0
Z=2(1)−3(0)=2−0=2
Z=2(4)−3(3)=8−9=−1
Z=2(2)−3(1)=4−3=1
Z=2(0)−3(1)=0−3=−3
- Z(A)=0
- Z(B)=2
- Z(C)=−1
- Z(D)=1
- Z(E)=−3
The minimum value of Z occurs at point E(0,1) where Z=−3.
The minimum value of Z is −3.
Topper's Solved these Questions
- SAMPLE PAPER (SELF-ASSESSMENT) -10BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER (SELF-ASSESSMENT) -10EXERCISE - SECTION - C
5 Videos
- SAMPLE PAPER (SELF-ASSESSMENT) -10BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER (SELF-ASSESSMENT) -10EXERCISE - SECTION - C
5 Videos
- CBSE TERM -1 SAMPLE PAPER 1BOOK - EDUCART PUBLICATIONCHAPTER - CBSE TERM -1 SAMPLE PAPER 1EXERCISE - SECTION - C
4 Videos
- SAMPLE PAPER - 5BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER - 5EXERCISE - Section - C
10 Videos
Similar Questions
The corner points of a feasible region determined by a system of linear inequations are (0,0),(4,0),(5,2),(2,2) and (0, 1). If the objective function is Z = x + y, then maximum of Z occurs at:
View SolutionThe corner points of a feasible region determined by a system of linear inequalities are (20,40),(50,100),(0,200) and (0,50). If the objective funtion Z=x+2y, then maximum of Z occurs at.
View Solution
Knowledge Check
The corner points of the feasible region determined by a system of linear inequations are (0,0),(4,0),(2,4) and (0,5). If the minimum value of Z=ax+by,a, b>0 occurs at (2,4) and (0,5) ,then :
Aa=2bB2a=bCa=bD3a=bIf the corner points of a feasible region of system of linear inequalities are (15,20) (40,15) and (2,72) and the objective function is Z = 6x + 3y then Zmax−Zmin =
A135B78C57D101The corner points of the feasible region determined by the system of linear contraints are (0,0), (0,40),( 20,40),(60,20),(60,0). The objective function is Z=4x+3y. Compare the quantity in Column A and Column B.
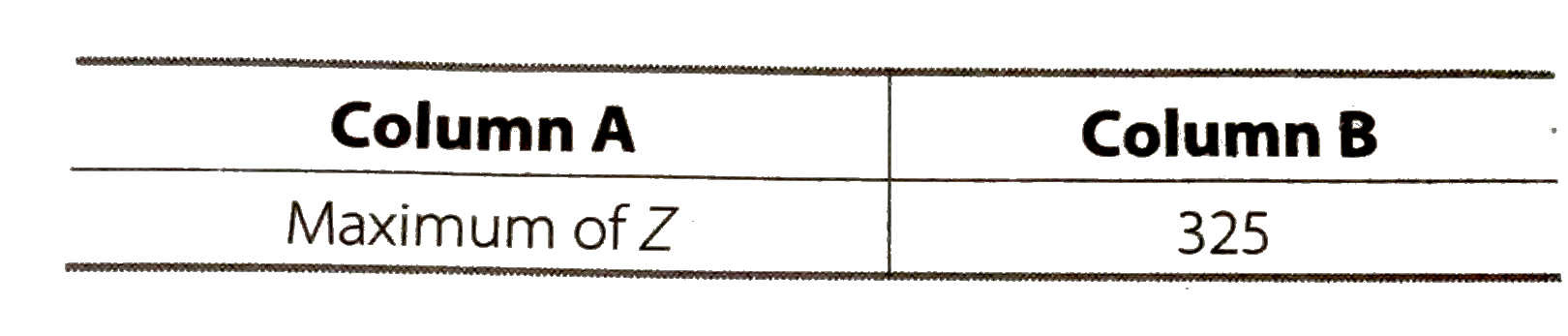 AThe quantity in Column A is greaterBThe quantity in column B is greaterCThe two quantities are equal.DThe relationship cannot be determined on the basis of the information supplied.
AThe quantity in Column A is greaterBThe quantity in column B is greaterCThe two quantities are equal.DThe relationship cannot be determined on the basis of the information supplied.
The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40). (20, 40), (60, 20). (60, 0). "The objective function is Z=4x+3y.
Compare the quantity in Column A and Column B.
Column AColumn BMaximum of Z325
View SolutionThe corner points of the feasible region of a system of linear inequalities are (0, 0), (4,0), (3,9), (1, 5) and (0, 3). If the maximum value of objective function, Z = ax + by occurs at points (3, 9) and (1, 5), then the relation between a and b is:
View SolutionThe corner points of the feasible region of the system of linear inequations x+y≥2,x+y≤5,x−y≥0,x,y≥0 are :
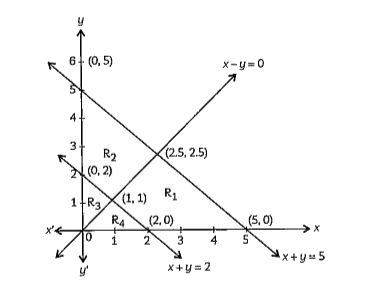
View SolutionThe corner points of the feasible region of a system of linear inequations are (0, 0), (5, 0), (6,5), (6, 8), (4, 10) and (0,8). If Z = 3x - 4y, then the minimum value of Z occurs at:
View SolutionThe carner points of the feasible region formed by the system of linear inequations x−y≥−1,−x+y≥0,x+y≤2andx,y≥0, are
View Solution