The corner points of the feasible region of the system of linear inequations $x + y \geq 2, x + y \leq 5, x - y \geq 0, x, y \geq 0$ are :

A

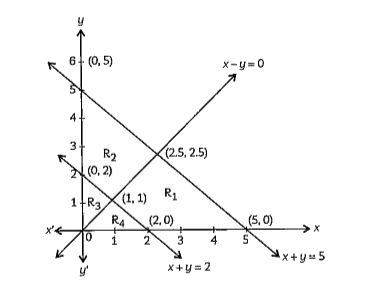
(0, 0), (2,0), (1, 1)

B

(0,2), (0,5), (1, 1), (2.5, 2.5)

C

(1, 1), (2.5, 2.5), (5,0), (2, 0)

D

(0,0), (1, 1), (0, 2)

Video Solution

|

Answer

Step by step video & image solution for The corner points of the feasible region of the system of linear inequations x+yge2,x+yle5,x-yge0,x,yge0 are : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The feasible region of the system of linear inequations $x + 2 y \leq 120, x + y \geq 60, x - 2 y \geq 0, x, y \geq 0$ :
Ais bounded and lies in first quadrant .
Bis unbounded and lies in first quadrant.
Cdoes in first quadrant .
Ddoes not exist.
Question 2 - Select One
The carner points of the feasible region formed by the system of linear inequations $x - y \geq - 1, - x + y \geq 0, x + y \leq 2 and x, y \geq 0$ , are
A $(0, 0), (- 1, 0), (0, 1)$
B $(0, 0), (2, 0), (1, 1)$
C $(0, 1), (1, 1), (0, 0)$
D $(0, 0), (1, 1), (\frac{1}{2}, \frac{3}{2}), (0, 1)$
Question 3 - Select One
The vertex of the linear inequalities $2 x + 3 y \leq 6, x + 4 y \leq 4, x \geq 0, y \geq 0$ is
A(1,0)
B(1,1)
C $\frac{12}{5}, \frac{2}{5}$
D $\frac{2}{5}, \frac{12}{5}$

EDUCART PUBLICATION-SAMPLE PAPER 09-SECTIONS-C

Home
Ask Doubt
Profile