The derivative of (logx)xw.r.txis(logx)x−1[1+logxlog(logx)]
R:ddx{f(x)g(x)[g(x)f'(x)f(x)+g'(x)log(f(x)] Solution in Telugu
Both A and R are true R is correct reason of A
Both A and R are treu R is not correct reason of A
A is true but R is false
A is false but R is true
The correct Answer is:A
Step by step video, text & image solution for The derivative of (log x) ^(x) w.r.t x is (log x)^(x-1) [1+ log x log (log x)] R : (d)/(dx) {f (x) ^(g(x))[g (x) (f'(x))/(f (x)) + g'(x) log (f(x) ] by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIATION BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIFFERENTIATION EXERCISE - SET-3
5 Videos
- DIFFERENTIAL EQUATIONSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Exercise 2
15 Videos
- DIRECTION COSINES AND DIRECTION RATIOSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIRECTION COSINES AND DIRECTION RATIOSEXERCISE - EXERCISE 2 SET -2
3 Videos
Similar Questions
Match the following
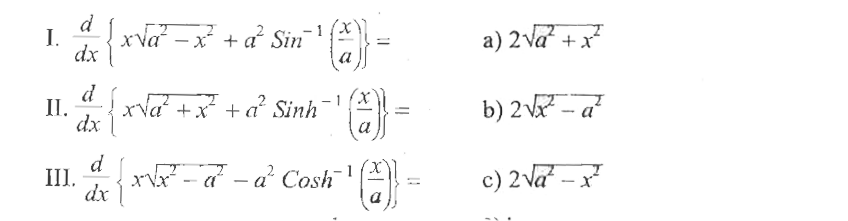
View SolutionI: The differential equation for the family of curves x2+y2−2ay=0, where a is an arbitraryconstantis (x2−y2)y'=2xy
II : The differential equation of the family of parabolas having vertices at the origin and foction y-axis is dydx=2yx
View SolutionIf the d.c.'s are (l, m, n) whose d.r's of a ray are (3, -4, 12) then ascending order of l, m, n is
View Solutionint_( is )((f(x)g'(x)-f'(x)g(x))/(f(x)g(x)))*(log(g(x))-log(f(x))dx
View SolutionThe differential coefficient of f(logx) with respect to x, where f(x)=logx is (a)xlogx (b) logxx (c) (xlogx)−1 (d) none of these
View Solutionint(f(x)*g'(x)-f'(x)g(x))/(f(x)*g(x)){log g(x)-log f(x)}dx
View SolutionIf f(x)=e^(sin(log cos x)) and g(x)=log cos x then what is the derivative of f(x)g(x)?
View SolutionIf function f and g given by
f(x)=log(x−1)−log(x−2)andg(x)=log(x−1x−2)are equal
then x lies in the interval.
View Solutionddx[tan−1(log(ex)log(e/x))]=1xf(x), then f(x)=
View Solution∫f(x)g'(x)−f'(x)g(x)f(x)g(x)[log(g(x))−log(f(x))]dx=
View SolutionIf log(f(x)) =g(x) then (d(f(x)))/(dx) =
View SolutionDifferentiate the following w.r.t. x :
f(x)=log[(2−x)1/2(x2−1)−1/4]
View SolutionLet f(x)=ln(x−1)(x−3) and g(x)=ln(x−1)+ln(x−3) then,
View Solution∫f(x)g'(x)−f'(x)g(x)f(x)g(x)[log(g(x))−log(f(x))]dx=
View SolutionThe function f(x)=log(x−1)−log(x−2) and g(x)=log(x−1x−2) are identical on
View Solution
