The diagonals AC and BD of a rhombus intersect at (5,6). If A≡(3,2), then find the equation of diagonal BD.
The correct Answer is:2y+x-17=0

mAC=6−25−3=2
or mBD=−12
Thus, the equation of BD is
(y−6)=−12(x−5)
i.e., 2y+x-17=0
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise 2.2
Explore 4 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise 2.3
Explore 7 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:JEE Advanced Previous Year
Explore 4 Videos
- STRAIGHT LINEBook:CENGAGEChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:JEE Advanced Previous Year
Explore 9 Videos
Similar Questions
Knowledge Check
The diagonals AC and BD of a rhombus intersect at (5, 6). If A (3, 2) then equation of diagonal BD is
Ay - x = 1B2 y - x = 17Cy - 2x + 4 = 0D2y + x = 17In a rhombus ABCD the diagonals AC and BD intersect at the point (3,4) . If the point A is (1,2) the diagonal BD has the equation
Ax−y−1=0Bx+y−1=0Cx−y+1=0Dx+y−7=0If one of the diagonals of a rhombus is 3x - 4y + 10 = 0 , then find the equation of the other diagonal which passes through point (−2,−3).
A4x + 3y + 17 = 0B3x - 4y + 15 = 0C4x + 3y - 15 = 0D3x - 4y - 11 = 0
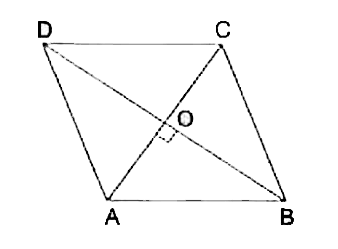
In the adjacent figure , ABCD is a rhombus whose diagonals AC and BD intersect at a point O. If side AB=10 cm and diagonal BD=16 cm , find the length of diagonal AC.
View SolutionThe sides of a rhombus are parallel to y=2x+3and2y=x+5 . The diagonals of the rhombus intersect at (1, 2). If one vertex of the rhombus lies on the y-axis then possible values of the ordinates of this vertex are 1 (b) 2 (c) 3 (d) 4
View SolutionThe diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
View SolutionTwo sides of a Rhombus ABCD are parallel to the lines x−y=5 and 7x−y=3. The diagonals intersect at (2,1) then the equations of the diagonals are
View SolutionThe diagonals of a rhombus are 7.5 cm and 12 cm. Findits area.
View Solution