The diagonals AC and BD of a cyclic quadrilateral ABCD interest at right angles at E (figure). A line l drawn through E and perpendicular to AB meets CD at F. Prove that F is the mid-point of CD.
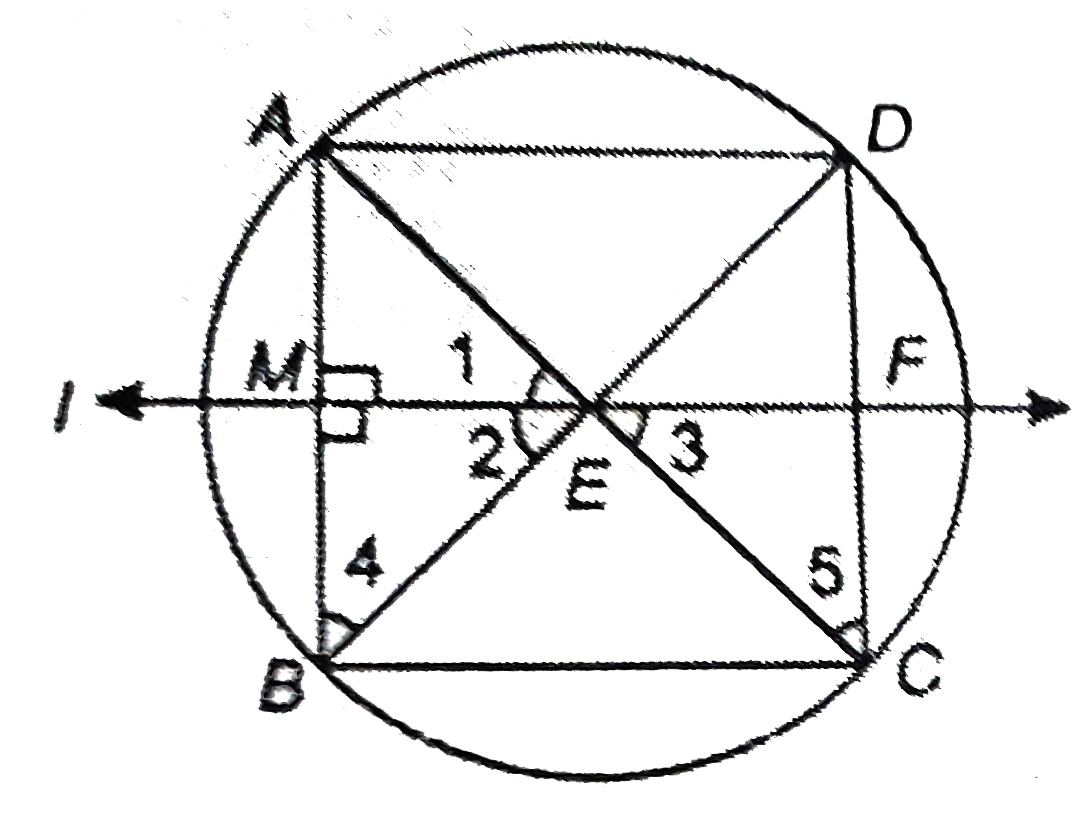
ABCD is a cyclic quadrilateral in which diagonals AC and BD intersect in E at right angles , l is a line through E and perpendicular to AB meets CD in F.
We have ∠AEB=90∘ (∵the diagonals are at right angles)
⇒∠1∠2=90∘
∠1=90∘−∠2 .....(1)
⇒∠1=90∘−∠2 (∵EM⊥AB)
Again ∠EMB=90∘
In ΔEMB, we have
∠2+∠4=90∘
⇒∠4=90∘−anl≥2 .......(2)
From eqs.(1) and (2) , we get
∠1=∠4
But ∠1=∠3 (vertically opposite angles)
∴∠3=∠4
Also, ∠4=∠5 (angles in the same segment of a circle are equal)
⇒∠3=∠5
⇒CF=EF (sides opposite to equal angles of a triangle are equal)
Similarly , DF=EF
⇒CF=DF
Hence, F is the mid-point of CD.
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
AB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
View SolutionE is the mid-point of the side AD of the tarapezium ABCD with AB∣∣DC. A line through E drawn parallel to AB intersects BC at F. Show that F is the mid-points of BC.
View Solution
Knowledge Check
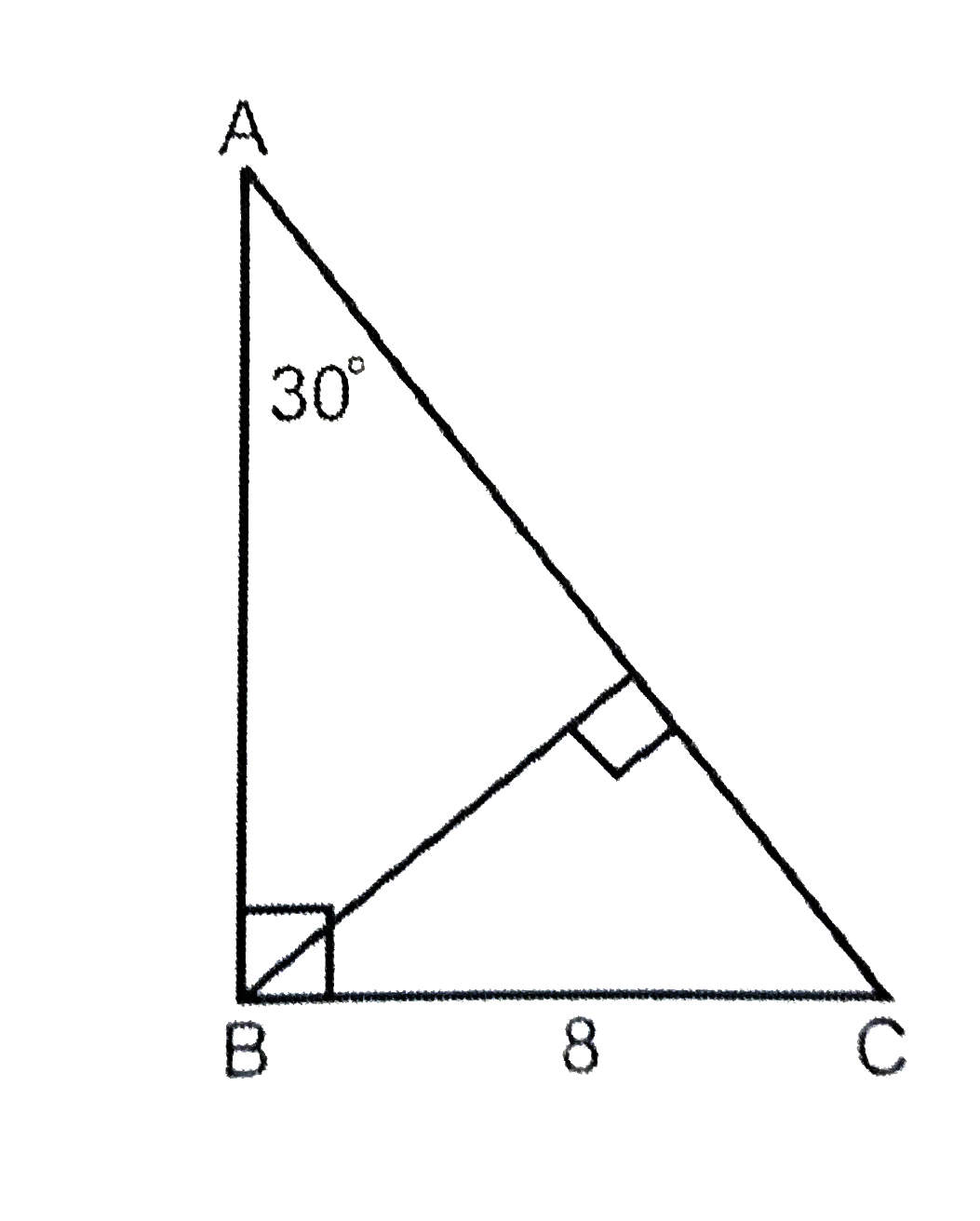
In the figure shown, ABC is a triangle, right angled at B. Through B, a line is drawn perpendicular to AC which meets AC in D. What is the length of BD?A4√3B8√3C2√3D4√3
D and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Prove that BDFE is a parallelogram
View SolutionThe diagonals of a quadrilateral intersect at right angles. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.
View SolutionIf ABCD is a cyclic quadrilateral, then prove that AC.BD=AB.CD+BC.AD
View SolutionIn triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
F is equidistant from AB and BC.
View SolutionIn a right triangle ABC, right angled at A, AD is drawn perpendicular to BC. Prove that:
AB2−BD2=AC2−CD2
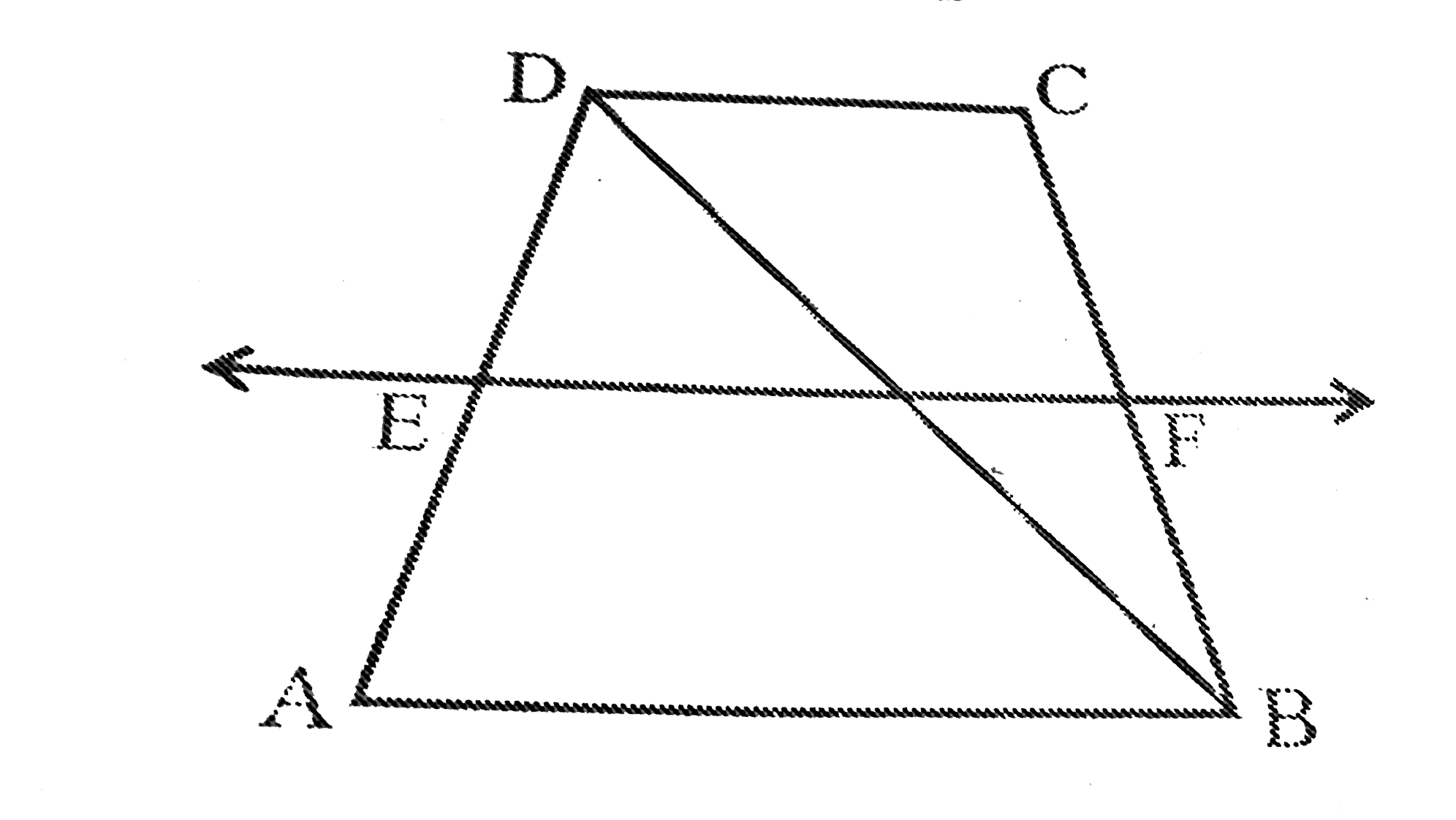
View SolutionABCD is a trapezium in which AB ∣∣ DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.
View SolutionIn a quadrilateral ABCD, it is given that AB∣∣CD and the diagonals ACandBD are perpendicular to each other. Show that AD.BC≥AB.CD.
View Solution
